Bonsoir,
je ne comprend pas ce qu'il faut faire à l'exercice 1 c de cette page si quelqu'un pourrait m'aider ce serait vraiment sympas:
http://coaching.epfl.ch/files/content/sites/coaching/files/groups/Coaching_SIE08/public/Anciens%20tests/Analyse/Enonc%C3%A9%20et%20corrig%C3%A9%20analyse%20test%201%202006.pdf
Arctan
6 messages
- Page 1 sur 1
Bonjour, :happy3:
Tu as le corrigé à la page $) de ton pdf :
de ton pdf :
Je reprends ce qui a été dit dans cette page :
Tu as : :
: 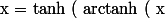 ) $)
Cette formule n'est rien d'autre que la formule : = \mathrm{id} (x) = x $) quant
quant  est bijective. ici :
est bijective. ici :  = \mathrm{tanh} (x) $) . :happy3:
. :happy3:
Ensuite, tu dérives les deux membres de l'égalité :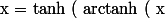 )$) en utilisant la formule de dérivation de composée de deux fonctions :
en utilisant la formule de dérivation de composée de deux fonctions : '(x) = f'(g(x)) g'(x) $) . Ici :
. Ici :  = \mathrm{tanh} (x) $) et
et  = \mathrm{arctanh} (x) $) .
.
Donc, on obtient :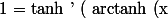 ) \mathrm{arctanh}' (x) $)
Ensuite, tu utilises la formule que tu devrais avoir dans ton cours ( c'est une identité remarquable qu'il faut mémoriser et la garder dans ton cerveau le jour où tu en auras besoin ) :
 = 1 - \mathrm{tanh}^2 (x) $)
et tu obtiens le résultat.
C'est à dire: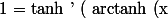 ) \mathrm{arctanh}' (x) $)
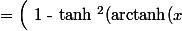 ) \Big) \mathrm{arctanh}' (x) = (1 - x^2 ) \mathrm{arctanh}' (x) $) , car :
, car :  ) = ( \mathrm{tanh} ( \mathrm{arctanh} (x) ) )( \mathrm{tanh} ( \mathrm{arctanh} (x) )) = x^2 $)
Cordialement. :happy3:
Tu as le corrigé à la page
Je reprends ce qui a été dit dans cette page :
Tu as :
Cette formule n'est rien d'autre que la formule :
Ensuite, tu dérives les deux membres de l'égalité :
Donc, on obtient :
Ensuite, tu utilises la formule que tu devrais avoir dans ton cours ( c'est une identité remarquable qu'il faut mémoriser et la garder dans ton cerveau le jour où tu en auras besoin ) :
et tu obtiens le résultat.
C'est à dire:
Cordialement. :happy3:
barbu23 a écrit:Bonjour, :happy3:
Tu as le corrigé à la pagede ton pdf :
Je reprends ce qui a été dit dans cette page :
Tu as ::
Cette formule n'est rien d'autre que la formule :quant
est bijective. ici :
. :happy3:
Ensuite, tu dérives les deux membres de l'égalité :en utilisant la formule de dérivation de composée de deux fonctions :
. Ici :
et
.
Donc, on obtient :
Ensuite, tu utilises la formule que tu devrais avoir dans ton cours ( c'est une identité remarquable qu'il faut mémoriser et la garder dans ton cerveau le jour où tu en auras besoin ) :
et tu obtiens le résultat.
C'est à dire:, car :
Cordialement. :happy3:
Merci beaucoup!! Je ne comprenais rien au corrigé aussi donc du coup voilà!! Mais merci :happy2: :happy2:
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
