Racines complexes d'un polynome

[BonbonB]

Bonjour,

Voilà, j'ai un petit exercice à faire mais je n'y arrive pas:

On considère le polynôme P(x)=x^6-3x^2-2.
On doit d'abord trouver le PGCD de P(x) et P'(x), puis en déduire les racines complexes de P(x) et ainsi sa factorisation en produit de puissances de polynômes irréductibles.

Alors la dérivée de P(x) est:P'(x)=6X^5-6X

Le PGCD de P(x) et P'(x) est:-2(x^2+1)

Merci :)

[wserdx]

Utilise le fait que le pgcd que tu viens de calculer divise P : calcule le quotient, ça te donnera un début de factorisation.

[BonbonB]

Ca me donne:
P(x) =((-1/2)x^4+(1/2)x^2+1)(-2(X²+1))

[Ben314]

Salut,
A SAVOIR (et à savoir démontrer vu que ça tient 2 lignes) : les racines du pgcd(P,P') sont les racines doubles de P.
Par exemple, ici, i et -i (les racines de X²+1) sont racines doubles de P ce qui signifie que P se factorise par ...

[BonbonB]

(x-i)^2 , (x+i)^2 ,du coup: (x-i) et (x+i) aussi...

Et donc après pour trouver les racines complexes de P(x), on résout:
((x-i)^2)* ((x+i)^2) * (x-i)* (x+i)=0 ?

[BonbonB]

Ce n'est pas ça? :doh:

[wserdx]

trouve maintenant les racines des facteurs. pour le facteur "bicarré" pense au changement de variable y=x au carré

[wserdx]

désolé, mon tuyau n'était pas complet. Comme le fait remarquer ben314, le PGCD est en facteur deux fois dans P

[wserdx]

Remarque : normalise tes facteurs en choisissant des polynômes unitaires.

[BonbonB]

ça veut dire quoi normaliser mes facteurs?

[wserdx]

ça veut juste dire de te ramener au polynôme dont le coefficient de tête vaut 1:
par exemple au lieu de considérer , prends à la place
C'est juste un détail, mais ça facilite les calculs!

[BonbonB]

OK donc il faut bien résoudre:
P(x)=0
((x-i)^2)* ((x+i)^2) * (x-i)* (x+i)=0
pour trouver les racines complexes ?

[Doraki]

((x-i)^2)* ((x+i)^2) * (x-i)* (x+i)= (x-i)^3 * (x+i)^3 = (x²+1)^3 = x^6 + 3x^4 + 3x² + 1, ce qui n'est pas P(x).

(x²+1)² est bien un diviseur de P, mais P n'est pas (x²+1)^3. Je sais pas pourquoi tu penses ça d'ailleurs.

[BonbonB]

Comment faire alors? :hein:

[Doraki]

Tu fais la division de P par (x²+1).
Ou alors tu cherches trois nombres a,b,c tels que P(x) = (x²+1)²(ax²+bx+c).

[BonbonB]

Tu fais la division de P par (x²+1).
Ou alors tu cherches trois nombres a,b,c tels que P(x) = (x²+1)²(ax²+bx+c).

P(x) =(x^2+1)(x^4-x^2-2)
Et là je résous:
(x^2+1)(x^4-x^2-2)=0 ?

[BonbonB]

Si ce n'est pas ça, aidez-moi s'il vous plait :cry:

[chan79]

Si ce n'est pas ça, aidez-moi s'il vous plait

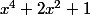
Divise par (qui est égal à

[BonbonB]

Comment vous trouvez x^4+2x^2+1 ?Pourquoi il faut faire ça?

[Doraki]

Tu as mis (x²+1) en facteur 1 fois dans P(x), mais tu sais que (x²+1) est en facteur 2 fois dans P (puisque i et -i sont racines doubles) donc il faut continuer. On sait que (x^4-x²-2) est encore un multiple de (x²+1) donc tu dois encore factoriser par (x²+1)