Fonction de classe k

[C.l]

Bonjour,

j'ai une question, comment fait-on pour montrer qu'une fonction est de classe k?

Merci d'avance

[barbu23]

Bonjour, :happy3:

On le fait par récurrence.

Cordialement. :happy3:

[barbu23]

Bonjour, :happy3:
En montrant que est fois dérivable, et que : est de classes .
Cordialement. :happy3:

[C.l]

Bonjour, :happy3:
En montrant que est fois dérivable, et que : est de classes .
Cordialement. :happy3:

Donc je dois la dérivée mais jusqu'ou? et comment je montre la dernière chose que vous avez mentionnez?

[barbu23]

Tu cherches l'expression de , dans ce cas là, on dit que est fois dérivable ou la dérivée - ième : existe. Après tu montres qu'elle est continue, c'est à dire de classe . :happy3:
Cordialement. :happy3:

Exemple : avec , on a et donc existe. Et il est clair qu'elle est continue car c'est un monôme d'un polynôme. :happy3:

[C.l]

Tu cherches l'expression de , dans ce cas là, on dit que est fois dérivable ou la dérivée - ième : existe. Après tu montres qu'elle est continue, c'est à dire de classe . :happy3:
Cordialement. :happy3:

Exemple : avec , on a et donc existe. Et il est clair qu'elle est continue car c'est un monôme d'un polynôme. :happy3:

merci :happy2: :happy2:

[barbu23]

Pas de quoi. :happy3:
Parfois, on nous demande de montrer que est de classe 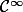, dans ce cas là, on le montre par récurrence. :happy3:
Je te dis ça pour que tu comprennes la différence qui existe entre est de classe et est de classe .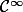
Cordialement. :happy3:

Exemple : .
est de classe .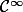
En effet, on procède par récurrence :
Pour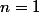 , est de classe . ( facile à montrer )
Ensuite, tu suppose que est de classe et tu montres que est de classe .