Relation liant les racines de P et de P'
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
LoUiSe
- Membre Naturel
- Messages: 10
- Enregistré le: 07 Sep 2006, 22:04
-
 par LoUiSe » 09 Sep 2006, 13:56
par LoUiSe » 09 Sep 2006, 13:56
Bonjour à tous, voici un exercice qui me pose problème depuis plusieurs jours et que je n'arrive pas à résoudre.
P est dans C[X] de degré n

sont les n racines de P. On suppose que

est racine simple de P.
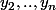
sont les n-1 racines de P'(polynôme dérivé de P).
il faut montrer
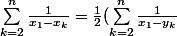)
Je sais déjà que
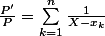
et
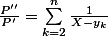
mais je ne vois pas comment obtenir l'égalité.
Je vous remercie d'avance pour l'aide que vous pourrez m'apporter.
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 09 Sep 2006, 14:15
par Flodelarab » 09 Sep 2006, 14:15
Que sont xk et yk ?
-
LoUiSe
- Membre Naturel
- Messages: 10
- Enregistré le: 07 Sep 2006, 22:04
-
 par LoUiSe » 09 Sep 2006, 14:17
par LoUiSe » 09 Sep 2006, 14:17
ce sont les racines de P (les
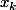
) et les racines de P' (les
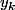
)

sont les n racines de P. On suppose que

est racine simple de P.
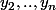
sont les n-1 racines de P'(polynôme dérivé de P)
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 09 Sep 2006, 15:44
par abcd22 » 09 Sep 2006, 15:44
Bonjour, je pense que ça marche en utilisant une façon différente de calculer
)
. On a
 = \sum_{i=1}^n\ \prod_{j \neq i} (X-x_j))
, donc
 = \prod_{i=2}^n (x_1 - x_i))
, et
 = \sum_{i=1}^n\ \sum_{j \neq i}\ \prod_{k \neq i,j} (X- x_k))
, on utilise cette expression pour calculer
)
et on obtient
}{P'(x_1)} = 2 \sum_{i=2}^n \frac{1}{x_1 - x_k})
.
-
LoUiSe
- Membre Naturel
- Messages: 10
- Enregistré le: 07 Sep 2006, 22:04
-
 par LoUiSe » 09 Sep 2006, 22:27
par LoUiSe » 09 Sep 2006, 22:27
Merci beaucoup abcd22, je n'avais pas pensé à chercher
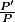
sous une autre forme. :happy2:
-
Vedeus
- Membre Naturel
- Messages: 39
- Enregistré le: 13 Juin 2006, 14:27
-
 par Vedeus » 10 Sep 2006, 09:19
par Vedeus » 10 Sep 2006, 09:19
Si vous le permettez, il y a moins bourrin.
Factorisez
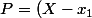Q)
, de sorte que
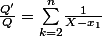
puis remarquez que
=Q'(x_1))
et
=2Q'(x_1))
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités