Série de Taylor
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
C.l
- Membre Relatif
- Messages: 109
- Enregistré le: 11 Juin 2013, 19:48
-
 par C.l » 11 Jan 2014, 18:39
par C.l » 11 Jan 2014, 18:39
Je bloque sur un exercice, qui demande d'écrire la série de Taylor de : cosx en xo=0
j'arrive à faire le polynôme de Taylor, mais pas à le mettre sous forme de série.. Quelqu'un pourrait m'éclaircir s'il vous plait?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 11 Jan 2014, 18:52
par barbu23 » 11 Jan 2014, 18:52
Bonsoir : :happy3:
La formule de Taylor au voisinage de

de la fonction
 = \cos (x) $)
est :
 = f(x_0) + \frac{f'(x_0 )}{1!} ( x-x_0 ) + \frac{f^{(2)} (x_0 )}{2!} (x-x_0 )^2 + \dots + \frac{f^{(n)} (x_0 ) }{n!} (x-x_0 )^n + \frac{f^{(n+1)} ( \xi )}{(n+1)!} (x-x_0)^{n+1} $)
avec

 = f(0) + f'(0) x + \frac{f''(0)}{2!} x^2 + \dots + \frac{f^{(n)} (0)}{n!} x^n + \frac{f^{(n+1)} ( \xi )}{(n+1)!} x^{n+1} $)
avec :

.
A toi de déterminer :
} (0) $)
Donc, la série de Taylor est :
} (0)}{n!} x^n $)
.
Cordialement. :happy3:
-
C.l
- Membre Relatif
- Messages: 109
- Enregistré le: 11 Juin 2013, 19:48
-
 par C.l » 11 Jan 2014, 19:22
par C.l » 11 Jan 2014, 19:22
barbu23 a écrit:Bonsoir : :happy3:
La formule de Taylor au voisinage de

de la fonction
 = \cos (x) $)
est :
 = f(x_0) + \frac{f'(x_0 )}{1!} ( x-x_0 ) + \frac{f^{(2)} (x_0 )}{2!} (x-x_0 )^2 + \dots + \frac{f^{(n)} (x_0 ) }{n!} (x-x_0 )^n + \frac{f^{(n+1)} ( \xi )}{(n+1)!} (x-x_0)^{n+1} $)
avec

 = f(0) + f'(0) x + \frac{f''(0)}{2!} x^2 + \dots + \frac{f^{(n)} (0)}{n!} x^n + \frac{f^{(n+1)} ( \xi )}{(n+1)!} x^{n+1} $)
avec :

.
A toi de déterminer :
} (0) $)
Donc, la série de Taylor est :
} (0)}{n!} x^n $)
.
Cordialement. :happy3:
Merci beaucoup d'avoir pris le temps de répondre. Dans mon corrigé j'ai un (-1)^n/ (2n)! je suppose que cest la même chose mais comment arrivez de votre forme à celle là?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 11 Jan 2014, 19:44
par barbu23 » 11 Jan 2014, 19:44
Cela découle du fait qu'il faut calculer d'abord
} (0) $)
pour obtenir ce résultat. :happy3:
-
C.l
- Membre Relatif
- Messages: 109
- Enregistré le: 11 Juin 2013, 19:48
-
 par C.l » 11 Jan 2014, 19:48
par C.l » 11 Jan 2014, 19:48
barbu23 a écrit:Cela découle du fait qu'il faut calculer d'abord
} (0) $)
pour obtenir ce résultat. :happy3:
Comment ça? Désolé je suis vraiment nul a comprendre ce genre de chose

-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 11 Jan 2014, 19:55
par barbu23 » 11 Jan 2014, 19:55
C.l a écrit:Comment ça? Désolé je suis vraiment nul a comprendre ce genre de chose

} (0) $)
est la dérivée

- ième de la fonction

en

.
On a :
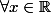
:
 = \cos (x) $)
Donc :
}(x) = (-1)^1 \sin (x) $)
} (x) = (-1)^1 \cos (x) $)
.
} (x) = (-1)^2 \sin (x) $)
} (x) = (-1)^2 \cos (x) $)
.
} (x) = (-1)^3 \sin (x) $)
} (x) = (-1)^3 \cos (x) $)
.



On cherche donc une relation de récurrence pour la dérivée

- ième de

qu'on note :
} (x) $)
à partir de ce qui précède. Quelle est cette relation ? En d'autres termes, combien vaut
} (x) $)
à partir de ce qui précède ?
Cordialement. :happy3:
-
C.l
- Membre Relatif
- Messages: 109
- Enregistré le: 11 Juin 2013, 19:48
-
 par C.l » 11 Jan 2014, 21:22
par C.l » 11 Jan 2014, 21:22
barbu23 a écrit:} (0) $)
est la dérivée

- ième de la fonction

en

.
On a :
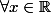
:
 = \cos (x) $)
Donc :
}(x) = (-1)^1 \sin (x) $)
} (x) = (-1)^1 \cos (x) $)
.
} (x) = (-1)^2 \sin (x) $)
} (x) = (-1)^2 \cos (x) $)
.
} (x) = (-1)^3 \sin (x) $)
} (x) = (-1)^3 \cos (x) $)
.



On cherche donc une relation de récurrence pour la dérivée

- ième de

qu'on note :
} (x) $)
à partir de ce qui précède. Quelle est cette relation ? En d'autres termes, combien vaut
} (x) $)
à partir de ce qui précède ?
Cordialement. :happy3:
} (x) $)
= (-1)^n cosx ou sin x ??
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 11 Jan 2014, 21:29
par barbu23 » 11 Jan 2014, 21:29
C'est presque ça :
} (x) = (-1)^n \cos (x) $)
} (x) = (-1)^{n+1} \sin (x) $)
.
Maintenant, tu calcules :
} (0 ) $)
et
} (0 ) $)
. :happy3:
-
C.l
- Membre Relatif
- Messages: 109
- Enregistré le: 11 Juin 2013, 19:48
-
 par C.l » 12 Jan 2014, 00:12
par C.l » 12 Jan 2014, 00:12
barbu23 a écrit:C'est presque ça :
} (x) = (-1)^n \cos (x) $)
} (x) = (-1)^{n+1} \sin (x) $)
.
Maintenant, tu calcules :
} (0 ) $)
et
} (0 ) $)
. :happy3:
Ce sera la même chose je ne comprend pas la différence? :-/
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 12 Jan 2014, 00:15
par barbu23 » 12 Jan 2014, 00:15
C.l a écrit:Ce sera la même chose je ne comprend pas la différence? :-/
} (x) $)
désigne
} (x) $)
,
} (x) $)
,
} (x) $)
... etc
} (x) $)
désigne
} (x) $)
,
} (x) $)
,
} (x) $)
... etc
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
de la fonction
est :
.
.
est la dérivée
- ième de la fonction
en
.
:
.
.
.
- ième de
qu'on note :
à partir de ce qui précède. Quelle est cette relation ? En d'autres termes, combien vaut
à partir de ce qui précède ?
