Produit de complexe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
eludante
- Membre Naturel
- Messages: 27
- Enregistré le: 29 Oct 2013, 17:19
-
 par eludante » 03 Jan 2014, 20:21
par eludante » 03 Jan 2014, 20:21
Merci pour ton aide Frede, j'avais aussi vu que lorsqu'on développait pour n=1 ou n=2 on avait bien la somme d'une suite géométrique
n=1 :
)
n=2 :
)
Mais lorsqu'on passe à
n=3 :
)
Et ce

nous gène
De même :
n=4 :
)
n=5 :
)
En tout cas merci pour tout ! Je vais continuer sur ta piste.
-
eludante
- Membre Naturel
- Messages: 27
- Enregistré le: 29 Oct 2013, 17:19
-
 par eludante » 03 Jan 2014, 20:48
par eludante » 03 Jan 2014, 20:48
J'ai l'impression qu'on ne peut pas trouver de formule explicite.
Car si on revient au résultat que j'avais trouvé (et que géotype a corrigé):
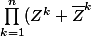=2^n\rho^{\frac{n(n+1)}{2}}\prod_{k=1}^{n}cos(k\theta))
On prend
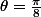
. Et bien pour
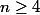
on trouvera que tout le produit est nul. Je vois donc difficilement comment on peut trouver une forme en fonction de

,

et

qui peut nous donner un résultat qui seras nul à partir d'un certain rang

pour certaine valeur de

...
-
eludante
- Membre Naturel
- Messages: 27
- Enregistré le: 29 Oct 2013, 17:19
-
 par eludante » 03 Jan 2014, 21:20
par eludante » 03 Jan 2014, 21:20
Bon, enfaîte je viens de comprendre qu'il faut exprimer tout ça en fonction de

et

uniquement et pas de

donc ça laisse entendre que
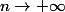
on devrait donc chercher cela :
)
avec

-
Frede
- Membre Naturel
- Messages: 55
- Enregistré le: 27 Déc 2013, 11:47
-
 par Frede » 04 Jan 2014, 08:50
par Frede » 04 Jan 2014, 08:50
OK, je vois mon erreur mais je ne désarme pas. Tu parais manier sans problème les arcanes de TEX. J'ai compris quelques petites choses en prenant un de tes messages et en regardant le code-source mais peut-être pourrais-tu me donner une indication sur un tutoriel qui existerait quelque part.
D'avance merci.
Frédé.
-
eludante
- Membre Naturel
- Messages: 27
- Enregistré le: 29 Oct 2013, 17:19
-
 par eludante » 04 Jan 2014, 13:33
par eludante » 04 Jan 2014, 13:33
Frede a écrit:OK, je vois mon erreur mais je ne désarme pas. Tu parais manier sans problème les arcanes de TEX. J'ai compris quelques petites choses en prenant un de tes messages et en regardant le code-source mais peut-être pourrais-tu me donner une indication sur un tutoriel qui existerait quelque part.
D'avance merci.
Frédé.
Tu trouveras tout ce dont tu as besoin sur
http://fr.wikipedia.org/wiki/Aide:Formules_TeXQuand tu utilise ^, il n'y auras que le prochain caractère qui seras mis en exposant. Il faut donc utiliser les accolades
Par exemple :
x^4 donne 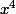
x^41 donne 
x^{41} donne 
x_{32} donne 
\sum_{k=1}^nk donne 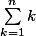
-
eludante
- Membre Naturel
- Messages: 27
- Enregistré le: 29 Oct 2013, 17:19
-
 par eludante » 04 Jan 2014, 16:38
par eludante » 04 Jan 2014, 16:38
Notre professeur ne nous a donner aucune indication, c'est un exercice d'un DM que je dois rendre Lundi. Si d'ici là je ne trouve pas la solution ce n'est pas bien grave mais je vous tiendrais au courant dès que j'aurais la correction.
-
eludante
- Membre Naturel
- Messages: 27
- Enregistré le: 29 Oct 2013, 17:19
-
 par eludante » 04 Jan 2014, 17:47
par eludante » 04 Jan 2014, 17:47
DM: Devoir Maison.
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 04 Jan 2014, 21:27
par Pythales » 04 Jan 2014, 21:27
eludante a écrit:Bonjour,
Pour faire cours, voici l'énoncé :Calculer
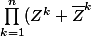)
(en fonction de

et

) avec

Donc calculer :
(Z^2+\overline Z^2)...(Z^n+\overline Z^n)) Mon avancement :
Mon avancement :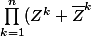=\prod_{k=1}^{n}\rho^k (e^{ik\theta}+e^{-ik\theta})=2^n\rho^{\frac{n(n+1)}{2}}\prod_{k=1}^{n}cos(k\theta))
Sachant que
=\frac {e^{ix}+e^{-ix}}{2})
J'aimerais de l'aide pour calculer ce produit de cosinus ou sinon une autre piste pourrait surement m'aider.
Merci
A exploiter :
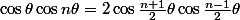
\theta=2\cos\frac{n+1}2\theta\cos\frac{n-1}2\theta)
\theta=2\cos\frac{n+1}2\theta\cos\frac{n-1}2\theta)
etc...
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 04 Jan 2014, 22:16
par jlb » 04 Jan 2014, 22:16
Pythales a écrit:A exploiter :
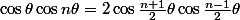
\theta=2\cos\frac{n+1}2\theta\cos\frac{n-1}2\theta)
\theta=2\cos\frac{n+1}2\theta\cos\frac{n-1}2\theta)
etc...
?????????????????? n=1 révolutionne les maths!
-
eludante
- Membre Naturel
- Messages: 27
- Enregistré le: 29 Oct 2013, 17:19
-
 par eludante » 04 Jan 2014, 23:59
par eludante » 04 Jan 2014, 23:59
Comment est-ce que tu trouve cela ?
J'ai essayer avec

et
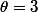
J'utilise :
cos(n\theta)=2cos(\frac{n+1}{2}\theta) cos(\frac{n-1}{2}\theta))
D'une part :
cos(2\times 3)\simeq -0.95)
D'autre part :
 cos(\frac{2-1}{2}\times 3) \simeq -0.03)
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 05 Jan 2014, 09:40
par Pythales » 05 Jan 2014, 09:40
eludante a écrit:Comment est-ce que tu trouve cela ?
J'ai essayer avec

et
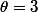
J'utilise :
cos(n\theta)=2cos(\frac{n+1}{2}\theta) cos(\frac{n-1}{2}\theta))
D'une part :
cos(2\times 3)\simeq -0.95)
D'autre part :
 cos(\frac{2-1}{2}\times 3) \simeq -0.03)
Au temps pour moi !
Ne tiens pas compte de ce message.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités