Restrictions
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Gonra
- Membre Relatif
- Messages: 100
- Enregistré le: 06 Déc 2012, 21:34
-
 par Gonra » 02 Jan 2014, 00:21
par Gonra » 02 Jan 2014, 00:21
bonsoir ,
je cherche la restriction de la fonction h à un intervalle [a,b]..je bloque sur la notion de restriction
h est une fonction de R dans R .strictement monotone.
on légalité : |h(x)-h(x')|>=|x-x'| pour tout couple x , x' de R.
[a,b] est un segment de R dont l'image par h est inclus dans [a,b].
h est supposée croissante.
j'ai montré que h(a)=a et h(b)=b , a et b sont des points fixes de h avec lénoncée
comme h(x) est strictement croissante(supposition) , h(a)Donc avec l'egalité de l'énoncée , h(x)-h(a)>= x-a Or h(a)=a donc h(x)>=x
de même h(x)-b <=x-b or h(b)=b Donc h(x)<=x
Finalement on a h(x)=x sur l'intervalle mais quelle est la restriction ?
Aussi je doit montrer que si h(x)>x alors h(x) équivaut à x en -infini
j'ai pensée au théorème de comparaison mais aucun utilité...
je peux montrer que h(x)=x étant donnée que h(x) est croissante et utilisée la définition de lÉquivalence ?
merci d'avance
-
jonses
- Membre Relatif
- Messages: 496
- Enregistré le: 19 Mai 2013, 09:33
-
 par jonses » 02 Jan 2014, 00:54
par jonses » 02 Jan 2014, 00:54
Gonra a écrit:
j'ai montré que h(a)=a et h(b)=b , a et b sont des points fixes de h avec lénoncée
Salut,
est-ce que ce serait possible que tu expliques comment tu obtiens ce résultat ?
-
Gonra
- Membre Relatif
- Messages: 100
- Enregistré le: 06 Déc 2012, 21:34
-
 par Gonra » 02 Jan 2014, 01:21
par Gonra » 02 Jan 2014, 01:21
jonses a écrit:Salut,
est-ce que ce serait possible que tu expliques comment tu obtiens ce résultat ?
la fonction h est croissante et [a,b] est un segment (a = 0 et h(b)-h(a)>=0
avec linégalité de l'énoncée :
|h(b)-h(a)|>=|b-a| (le cas a-b=b-a
comme h([a,b]) est inclus dans [a,b] , l'intervalle est stable par h
donc à fortiori h(b)-h(a)=b-a et h(b)-h(a)<= b-a
qui implique h(b)-h(a)=b-a
h(b)=b h(a)=a
-
jonses
- Membre Relatif
- Messages: 496
- Enregistré le: 19 Mai 2013, 09:33
-
 par jonses » 02 Jan 2014, 01:38
par jonses » 02 Jan 2014, 01:38
Gonra a écrit:la fonction h est croissante et [a,b] est un segment (a = 0 et h(b)-h(a)>=0
avec linégalité de l'énoncée :
|h(b)-h(a)|>=|b-a| (le cas a-b=b-a
comme h([a,b]) est inclus dans [a,b] , l'intervalle est stable par h
donc à fortiori h(b)-h(a)=b-a et h(b)-h(a)=|x-x'| pour tout couple x , x' de R.
[a,b] est un segment de R dont l'image par h est inclus dans [a,b].
h est supposée croissante.
j'ai montré que h(a)=a et h(b)=b , a et b sont des points fixes de h avec lénoncée
comme h(x) est strictement croissante(supposition) , h(a)= x-a Or h(a)=a donc h(x)>=x
de même h(x)-b x alors h(x) équivaut à x en -infini
j'ai pensée au théorème de comparaison mais aucun utilité...
je peux montrer que h(x)=x étant donnée que h(x) est croissante et utilisée la définition de lÉquivalence ?
merci d'avance
Je réfléchis, mais vu mon état de fatigue...
-
Gonra
- Membre Relatif
- Messages: 100
- Enregistré le: 06 Déc 2012, 21:34
-
 par Gonra » 02 Jan 2014, 14:10
par Gonra » 02 Jan 2014, 14:10
quelquun aurait une piste svp ?
-
Rha
- Membre Naturel
- Messages: 51
- Enregistré le: 21 Oct 2013, 22:35
-
 par Rha » 02 Jan 2014, 15:00
par Rha » 02 Jan 2014, 15:00
Bonjour,
Pour la question sur l'équivalence, tu ne peux pas montrer que
 = x)
à partir de la croissante de

(ça serait assez contradictoire vu que tu supposes
 > x)
).
En revanche tu peux montrer quelque chose de similaire qui permet de conclure avec le "théorème des gendarmes".
A tous les coup c'est ce que tu as déjà fait mais avec une faute d'étourderie, reprends le raisonnement.
-
Gonra
- Membre Relatif
- Messages: 100
- Enregistré le: 06 Déc 2012, 21:34
-
 par Gonra » 02 Jan 2014, 15:43
par Gonra » 02 Jan 2014, 15:43
Rha a écrit:Bonjour,
Pour la question sur l'équivalence, tu ne peux pas montrer que
 = x)
à partir de la croissante de

(ça serait assez contradictoire vu que tu supposes
 > x)
).
En revanche tu peux montrer quelque chose de similaire qui permet de conclure avec le "théorème des gendarmes".
A tous les coup c'est ce que tu as déjà fait mais avec une faute d'étourderie, reprends le raisonnement.
mais on suppose plus que h([a,b])=[a;b]
on sait juste qu'elle est croissante stricte et que h(x)>x qu'elle que soit le réel x dans R
et que |h(x)-h(x')|>=|x-x'| pour tout couple x , x' de R.
j'ai testé :
h(x)>x posons h(x)=y
y>x
donc
h(y)>h(x) par croissance
h(y)-h(x)>0 et y-x>0
|h(y)-h(x)| >= |y-x| en posant x=y et x'=x
h(y)-h(x) >= y-x>0
h(y)-y >= h(x)-x >0
h(h(x))-h(x)>=h(x)-x>0
je suis perdu..
-
Rha
- Membre Naturel
- Messages: 51
- Enregistré le: 21 Oct 2013, 22:35
-
 par Rha » 02 Jan 2014, 17:05
par Rha » 02 Jan 2014, 17:05
Essaie de montrer que
 \leq x + h(0))
.
-
Gonra
- Membre Relatif
- Messages: 100
- Enregistré le: 06 Déc 2012, 21:34
-
 par Gonra » 02 Jan 2014, 18:13
par Gonra » 02 Jan 2014, 18:13
on pose x'=x et x=0 donc
-h(x)| \leq |0-x|)
pour

est positif donc

et comme h est croissante alors pour
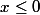
 \geq h(x))
donc
-h(x) \geq 0)
donc
-h(x) \geq x)
-h(0) \leq x)
 \leq x+h(0))
De même , si
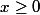
on a, en posant

,
-h(0)|\geq x-0)
 \geq x+h(0))
donc
 \geq h(x) \geq x+h(0))
h(x) equivalent à x en

si
>x)
et en

si
<x)
-
jonses
- Membre Relatif
- Messages: 496
- Enregistré le: 19 Mai 2013, 09:33
-
 par jonses » 02 Jan 2014, 18:23
par jonses » 02 Jan 2014, 18:23
Bah là tu as ce qu'il faut pour obtenir l'équivalent en - l'infini, non ? :
Tu as obtenu pour
}{x}\ge 1+\frac{h(0)}{x})
puis gendarmes quand

tend vers - l'infini
Gonra a écrit:donc
 \geq h(x) \geq x+h(0))
Je vois pas comment tu obtiens ça, la variable x n'est pas la même pour montrer
 \geq h(x))
que pour montrer
 \geq x+h(0))
, non ?
-
Gonra
- Membre Relatif
- Messages: 100
- Enregistré le: 06 Déc 2012, 21:34
-
 par Gonra » 02 Jan 2014, 18:28
par Gonra » 02 Jan 2014, 18:28
ah oui c'est exact...:marteau:
Merci pour votre Aides Rha et Jonses !!
Bonne année/soirée
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
