Devoir maison (terminale S)

[kelly65]

Bonjour, j'ai un devoir maison à faire pour la rentrée et je n'arrive pas à faire la partie B

Voilà l'énoncé :
On considère la suite () définie sur N par :
= alpha (sachant que 0.02 alpha 0.03) et =

1) Montrer par récurrence que la suite est à valeurs positives
2) Montrer que la suite () est décroissante
3) En déduire que la suite () est convergente. Quelle est sa limite ?

J'ai essayé de chercher mais je n'y arrive pas

[kelly65]

Besoin d'aide s'il vous plait

[ampholyte]

Bonjour,

As-tu fait quelque chose ou as-tu quelques choses à nous montrer ?

[kelly65]

Bonjour,

As-tu fait quelque chose ou as-tu quelques choses à nous montrer ?

Question 1 :
Initialisation
=
donc = 0.02
et si on prends 0.03 cela donne 0.03

Hérédité
Après je sais pas comment faire

[ampholyte]

En fait il ne faut pas utiliser de valeur mais plutôt alpha.

1 - Initialisation :



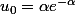
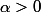
par définition et car la fonction exponentielle est strictement positif sur R alors le produit est positif.

2 - Hérédité
Supposons que un > 0, montrons que



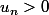
car la fonction exponentielle est strictement positive

Le produit est donc positif :

[FDH]

Bjr

attention les réponses fournies sont bien loin d'être correctes ....
la rédaction est importante,
déja évite les erreurs de Français, Héréditée ( tu démontre une proposition, donc feminin)

tu as 3 pts a demontrer:

<1> Initialisation
<2> Hériditée
<3> Conclusion

si tu veux plus de détails contacte moi
FDH

[kelly65]

Merci beaucoup pour vos réponses

[kelly65]

Pour la question 2 :
il faut montrer que Un+1 - Un est inférieur à 0 c'est ça ?

[FDH]

oui, inférieur ou égal à zéro ( décroissant)

[kelly65]

oui, inférieur ou égal à zéro ( décroissant)

Donc
Je fais quoi après ? J'ai vraiment du mal là -_- c'est tout bête mais bon...

[chan79]

Donc
Je fais quoi après ? J'ai vraiment du mal là -_- c'est tout bête mais bon...

salut et bonne année

si

[kelly65]

salut et bonne année

si

Tu peux m'expliquer comment tu trouves ça ?

[FDH]

aie...non
(Un+1)-(Un)= (Unxe^-Un)-(Un)
= Un( e^-Un -1)

or Un sup ou egal à zéro, donc ça dépend de e^-Un -1

e^-Un= 1/e^Un donc e^-Un -1 <0

si tu as skype c'est plus simple pour te répondre ou t'envoyé un fichier manuscrit

[kelly65]

Merci beaucoup FDH j'ai compris

[kelly65]

Maintenant je dois écrire un algorithme qui possède pour valeur d'entrée un réel e (e pour écart) et qui donne en sortie le rang tel que si , alors

Besoin d'aide s'il vous plait je n'y arrive pas

[kelly65]

Besoin d'aide pour l'algorithme s'il vous plait

[kelly65]

C'est urgent je dois rendre demain !
Quelqu'un pour m'aider pour l'algorithme ????

[kelly65]

Maintenant je dois écrire un algorithme qui possède pour valeur d'entrée un réel e (e pour écart) et qui donne en sortie le rang tel que si , alors

Besoin d'aide s'il vous plait je n'y arrive pas

[Sylviel]

Bonjour,

réfléchissons un peu : si Un est décroissante il te suffit de trouver le premier n tel que
Un < e non ?
Donc l'algo consiste à trouver ce premier Un. Pour cela il suffit de
- calculer Un
- comparer à e
- si c'est bon on arrête, sinon on passe à n+1

ok ?

[kelly65]

J'ai compris
Merci beaucoup Sylviel