Limite coriace
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 31 Déc 2013, 15:11
par barbu23 » 31 Déc 2013, 15:11
Bonjour, :happy3:
J'appelle à votre aide pour calculer :
 | $)
.
J'ai pensé utiliser le TAF
Voici comment :
Sur l'intervalle :

:
 = \sin (t) $)
est continue et sur l'intervalle

,

est dérivable, donc :

telle que :
 - \sin (0 ) = \cos (c) (n-0) $)
Donc,
 | \leq n $)
, car
 | \leq 1 $)
.
Mais, celà n'aboutit pas.
Merci d'avance. :happy3:

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 31 Déc 2013, 15:48
par Ericovitchi » 31 Déc 2013, 15:48
non, la méthode est plutôt de raisonner par l'absurde. Suppose que la limite existe et montre que l'on tombe sur une absurdité (en utilisant cos²n+sin²n=1 ou sin 2n = 2 sin n cos n ) et déduis-en que la suite n'a pas de limite.
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 31 Déc 2013, 15:49
par L.A. » 31 Déc 2013, 15:49
Bonjour.
Tu es très mal parti, ta majoration
| \leq n)
ne sert pas à grand chose puisque on sait déjà que
| \leq 1)
...
Il faut plutôt montrer que la limite n'existe pas, étant donné que la suite admet pour valeurs d'adhérence tous les réels entre 0 et 1. Pars du fait que le groupe

est dense dans

.
Edit : Ma méthode est sûrement plus compliquée que celle d'Ericovitchi :triste:
-
Rha
- Membre Naturel
- Messages: 51
- Enregistré le: 21 Oct 2013, 22:35
-
 par Rha » 31 Déc 2013, 16:01
par Rha » 31 Déc 2013, 16:01
C'est une limite très coriace!
Pour compléter un tout petit peu:
Une application de la caractérisation des sous-groupes additifs de

permet de montrer que si

et

sont deux réels dont l'un est rationnel et l'autre irrationnel,

est dense dans

.
On peut en déduire que pour tout entier naturel

,
 - |\alpha| \ |]-\infty;N|])
est dense dans

.
(en général pour

et

deux parties denses d'un espace topologique quelconque, l'une des deux étant ouverte,
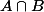
est dense)
Cela permet de montrer l'existence de suites strictement croissantes de d'entiers naturels (i.e. d'extractrices) dont le produit par

se rapproche autant qu'on veut de n'importe quel réel modulo

.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 31 Déc 2013, 16:04
par barbu23 » 31 Déc 2013, 16:04
Merci pour ces précisions à vous deux @L.A. et @Ericovitchi. :we:
Si on suit d'abord la méthode de @L.A. :
Pourquoi :

?
Soit

:
Pourquoi

:
 \bigcap \mathbb{Z} + 2 \pi \mathbb{Z} \neq \emptyset $)
?
Edit : Merci à toi aussi @Rha. Je vais lire ce que tu as écrit. :we:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 31 Déc 2013, 17:20
par barbu23 » 31 Déc 2013, 17:20
Merci pour ces précisions à vous deux @L.A. et @Ericovitchi. :we:
Si on suit d'abord la méthode de @L.A. :
Pourquoi :

?
Soit

:
Pourquoi

:
 \bigcap \mathbb{Z} + 2 \pi \mathbb{Z} \neq \emptyset $)
?
Edit : Merci à toi aussi @Rha. Je vais lire ce que tu as écrit. :we:
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 31 Déc 2013, 17:56
par nodjim » 31 Déc 2013, 17:56
Vu le n qui tourne sur le cercle trigonométrique, c'est plutôt immédiat l'absence de limite, non ?
-
Losange
- Membre Naturel
- Messages: 60
- Enregistré le: 14 Nov 2013, 23:51
-
 par Losange » 31 Déc 2013, 21:11
par Losange » 31 Déc 2013, 21:11
Il me semble plus simple de trouver deux sous-suites qui ne peuvent pas tendre vers la même limite.
Soit
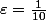
.
Je propose
=\lfloor 2\pi n+\frac{3\pi}{4}-\varepsilon \rfloor)
=\lfloor 2\pi n+\frac{5\pi}{4}-\varepsilon \rfloor)
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 31 Déc 2013, 21:26
par deltab » 31 Déc 2013, 21:26
Bonsoir et Bonne année à toutes et à tous avec mes meilleurs vux.
Losange a écrit:Il me semble plus simple de trouver deux sous-suites qui ne peuvent pas tendre vers la même limite.
Soit
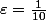
.
Je propose
=\lfloor 2\pi n+\frac{3\pi}{4}-\varepsilon \rfloor)
=\lfloor 2\pi n+\frac{5\pi}{4}-\varepsilon \rfloor)
Crois tu qu'on puisse utiliser les
)
donnés, la manipulation des parties entières est toujours délicate.
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 31 Déc 2013, 21:39
par deltab » 31 Déc 2013, 21:39
@ Rha
Je préfère utiliser la méthode préconisée par Ericovitchi. Elle a l'avantage de rester 'terre à terre" donc plus accessible et ne nécessite pas une connaisse approfondie de la topologie de

.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 31 Déc 2013, 22:02
par barbu23 » 31 Déc 2013, 22:02
deltab a écrit:@ Rha
Je préfère utiliser la méthode préconisée par Ericovitchi. Elle a l'avantage de rester 'terre à terre" donc plus accessible et ne nécessite pas une connaisse approfondie de la topologie de

.
Je ne sais pas comment.

Supposons que

:
 | = a $)
On pose

telle que
 = 2n $)
Alors :
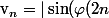 )| $)
est une suite extraite de
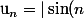 | $)
qui converge vers

( i.e :
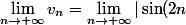| = \displaystyle \lim_{n \to + \infty} 2 |\sin (n)| |\cos (n)| = 2a \sqrt{1 - a^{2}} \neq a $)
)
Contradiction ? :doh:
Merci d'avance. :happy3:
-
Losange
- Membre Naturel
- Messages: 60
- Enregistré le: 14 Nov 2013, 23:51
-
 par Losange » 31 Déc 2013, 22:51
par Losange » 31 Déc 2013, 22:51
Losange a écrit:Il me semble plus simple de trouver deux sous-suites qui ne peuvent pas tendre vers la même limite.
Soit
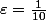
.
Je propose
=\lfloor 2\pi n+\frac{3\pi}{4}-\varepsilon \rfloor)
=\lfloor 2\pi n+\frac{5\pi}{4}-\varepsilon \rfloor)
Je détaille :
-2\pi\geq \frac{\pi}{4}+\varepsilon)
et
-2\pi\geq \frac{3\pi}{4}+\varepsilon)
On en déduit que
| \geq \sin(\frac{\pi}{4}+\varepsilon))
et
| \leq \sin(\frac{\pi}{4}-\varepsilon))
D'où
| \geq \sin(\frac{\pi}{4}+\varepsilon)>\frac{\sqrt{2}}{2}> \sin(\frac{\pi}{4}-\varepsilon)\geq |\sin(\psi(n)|)
Si
|)
avait une limite elle serait strictement plus grande et strictement plus petite que
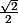
. Contradiction.
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 01 Jan 2014, 00:03
par deltab » 01 Jan 2014, 00:03
BONNE ANNEE!!! AVEC TOUS MES VOEUX
-
Rha
- Membre Naturel
- Messages: 51
- Enregistré le: 21 Oct 2013, 22:35
-
 par Rha » 01 Jan 2014, 13:47
par Rha » 01 Jan 2014, 13:47
@deltab:
Tout à fait, ces connaissances sont inutilement "avancées" pour cette question.
En revanche, elles permettent de d'aider à traiter le cas de fonctions périodiques continues quelconques.
Et puis bonne année :)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
.
.