Partie entière et racine carrée
24 messages
- Page 1 sur 2 - 1, 2
Partie entière et racine carrée
Bonjour, un petit problème sur les parties entières qui me donne du fil à retordre, pourtant ça ne m'avais pas l'air bien compliqué :
(nb: Va' désigne la racine carrée de a)
"Déterminer pour tout entier naturel n non nul [Vn' + Vn+1']=[V4n+2'] "
J'ai utilisé la définition de la partie entière et posé p Vn' + Vn+1' < p+1 et q V4n+2' < q+1
En combinant les inégalités j'ai essayé de montrer que p-q ou q-p=0 mais sans réussite donc je suis parti sur la manipulation de la première inégalité pour tenter d'aboutir à la deuxième et montrer que p est aussi partie entière de V4n+2':
0 p Vn' + Vn+1' < p+1
p² 2n+1 + V4n²+4n' < (p+1)²
p² 2n+1 +V(2n+1)²-1' < (p+1)²
Là, j'ai bien envie de montrer que 2n+1 + V(2n+1)²' < (p+1)² ( le coté gauche de l'inégalité s'obtient a fortiori) et ainsi dire p² 4n+2 < (p+1)² ainsi p = [V4n+2'].
Pour ce faire je veux montrer que (1): 0 < 2n+1 - V(2n+1)²-1' < 1 et que (2) : 2n+1 + V(2n+1)²-1' < p²+ 2p
J'ai maladroitement obtenu la (1) mais je bloque sur la (2)
Cette méthode me parait assez laborieuse et peu esthétique donc je me demandais si j'étais sur la bonne voie ... n'y a-t-il pas des manipulations plus simple à faire sur les inégalités ?
Merci pour votre attention devant ce texte peu lisible (les racines n'aident pas) et merci pour votre éventuelle aide.
(nb: Va' désigne la racine carrée de a)
"Déterminer pour tout entier naturel n non nul [Vn' + Vn+1']=[V4n+2'] "
J'ai utilisé la définition de la partie entière et posé p Vn' + Vn+1' < p+1 et q V4n+2' < q+1
En combinant les inégalités j'ai essayé de montrer que p-q ou q-p=0 mais sans réussite donc je suis parti sur la manipulation de la première inégalité pour tenter d'aboutir à la deuxième et montrer que p est aussi partie entière de V4n+2':
0 p Vn' + Vn+1' < p+1
p² 2n+1 + V4n²+4n' < (p+1)²
p² 2n+1 +V(2n+1)²-1' < (p+1)²
Là, j'ai bien envie de montrer que 2n+1 + V(2n+1)²' < (p+1)² ( le coté gauche de l'inégalité s'obtient a fortiori) et ainsi dire p² 4n+2 < (p+1)² ainsi p = [V4n+2'].
Pour ce faire je veux montrer que (1): 0 < 2n+1 - V(2n+1)²-1' < 1 et que (2) : 2n+1 + V(2n+1)²-1' < p²+ 2p
J'ai maladroitement obtenu la (1) mais je bloque sur la (2)
Cette méthode me parait assez laborieuse et peu esthétique donc je me demandais si j'étais sur la bonne voie ... n'y a-t-il pas des manipulations plus simple à faire sur les inégalités ?
Merci pour votre attention devant ce texte peu lisible (les racines n'aident pas) et merci pour votre éventuelle aide.
Salut !
J'ai du mal à comprendre ton énoncé :
Il faut trouver les valeurs de qui vérifient cette égalité, ou il faut montrer cette égalité pour tout
qui vérifient cette égalité, ou il faut montrer cette égalité pour tout  ?
?
ttk a écrit:"Déterminer pour tout entier naturel n non nul [Vn' + Vn+1']=[V4n+2'] "
J'ai du mal à comprendre ton énoncé :
Il faut trouver les valeurs de
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Bonsoir,
Votre problème est très intéressant enfin du moins il m'a intéressé aussi.
Voilà comment je continue : d'après le point 3
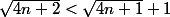
donc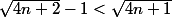
d'où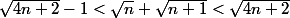
mais peut on pour autant conclure ?
On a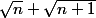 qui est élément de [p;p+1[ et aussi de
qui est élément de [p;p+1[ et aussi de 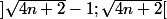
deux intervalles de longueur 1 qui ne sont pas disjoints puisque leur intersection contient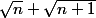 .
.
Mais là où j'ai un problème c'est que l'on peut avoir dans cet ordre :
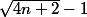 , p ,
, p , 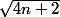 , p+1 et là ça marche.
, p+1 et là ça marche.
mais on peut avoir aussi
p ,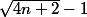 , p+1 ,
, p+1 , 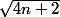 et là cela ne va plus du tout.
et là cela ne va plus du tout.
Pourquoi ce deuxième cas est il impossible ?
Votre problème est très intéressant enfin du moins il m'a intéressé aussi.
Voilà comment je continue : d'après le point 3
donc
d'où
mais peut on pour autant conclure ?
On a
deux intervalles de longueur 1 qui ne sont pas disjoints puisque leur intersection contient
Mais là où j'ai un problème c'est que l'on peut avoir dans cet ordre :
mais on peut avoir aussi
p ,
Pourquoi ce deuxième cas est il impossible ?
nodjim a écrit:Si le problème est: trouver tous les n tel que [Vn+V(n+1)]=[V(4n+2)] alors la réponse semble être:
Egalité dans les intervalles [n²-1;n²+n-1]
Mais je ne sais pas si c'est le vrai problème...
J'étais tombé sur ce problème (que j'avais pas réussi à résoudre d'ailleurs) et l'énoncé était de montrer que l'égalité est vérifiée (pour n dans N) lorsque 4n+2 n'est pas le carré d'un entier mais ils précisaient en remarque que ce n'était jamais le cas et donc vrai sans hypothèse supplémentaires (c'est juste utile pour la démo). C'est dans le cours d'arithmétique d'animaths si vous voulez le corrigé.
Tiruxa a écrit:Mais là où j'ai un problème c'est que l'on peut avoir dans cet ordre :, p ,
, p+1 et là ça marche.
mais on peut avoir aussi
p ,, p+1 ,
et là cela ne va plus du tout.
Pourquoi ce deuxième cas est il impossible ?
Peut on conclure même si le 2è cas est démontré impossible ? Car il faut qu'on ait l'infériorité STRICTE de
Une autre approche.
[Vn+V(n+1)]=[V(4n+2)]
C'est vrai si l'incrémentation des parties entières se fait pour le même n pour les 2 expressions. L'incrémentation se fait quand on dépasse un carré parfait.
Pour un carré pair, que vaut n dans V(4n+2) ?
4n+2=4k²
n=k²-1/2 donc comme n entier, il faut n=k²
Pour n=k², l'incrémentation se fait elle dans l'expresion [Vn+V(n+1)] ?
Vk²+V(k²+1)>2k
Mais il faut vérifier que l'incrémentation ne se fait pas pour n=k²-1
V(k²-1)+Vk²<2k
C'est donc Ok pour un carré pair.
Pour un carré impair
4n+2=4k²+4k+1
n=k²+k-1/4 donc n=k²+k
V(k²+k)+V(k²+k+1)>? 2k+1=2V(k²+k+1/4)
V(k²+k+1)-V(k²+k+1/4)>? V(k²+k+1/4)-V(k²+k)
On pose x=k²+k+1/4
V(x+3/4)-Vx >? Vx-V(x-1/4)
V(x+3/4)+V(x-1/4)>?2Vx
2x+1/2+2V(x+3/4)(x-1/4)>?4x
V(x+3/4)(x-1/4)>?x-1/4
(x+3/4)(x-1/4)>?x²-x/2+1/16
x²+x/2-3/16>?x²-x/2+1/16
x>?1/4
tjs vrai.
Il faut aussi vérifier que pour n=k²+k-1 Vn+V(n+1)<2k+1=2V(k²+k+1/4)
Ici, la lecture directe le prouve.
V(k²+k-1)+V(k²+k)<2V(k²+k+1/4).
C'est donc OK aussi pour un carré impair.
[Vn+V(n+1)]=[V(4n+2)]
C'est vrai si l'incrémentation des parties entières se fait pour le même n pour les 2 expressions. L'incrémentation se fait quand on dépasse un carré parfait.
Pour un carré pair, que vaut n dans V(4n+2) ?
4n+2=4k²
n=k²-1/2 donc comme n entier, il faut n=k²
Pour n=k², l'incrémentation se fait elle dans l'expresion [Vn+V(n+1)] ?
Vk²+V(k²+1)>2k
Mais il faut vérifier que l'incrémentation ne se fait pas pour n=k²-1
V(k²-1)+Vk²<2k
C'est donc Ok pour un carré pair.
Pour un carré impair
4n+2=4k²+4k+1
n=k²+k-1/4 donc n=k²+k
V(k²+k)+V(k²+k+1)>? 2k+1=2V(k²+k+1/4)
V(k²+k+1)-V(k²+k+1/4)>? V(k²+k+1/4)-V(k²+k)
On pose x=k²+k+1/4
V(x+3/4)-Vx >? Vx-V(x-1/4)
V(x+3/4)+V(x-1/4)>?2Vx
2x+1/2+2V(x+3/4)(x-1/4)>?4x
V(x+3/4)(x-1/4)>?x-1/4
(x+3/4)(x-1/4)>?x²-x/2+1/16
x²+x/2-3/16>?x²-x/2+1/16
x>?1/4
tjs vrai.
Il faut aussi vérifier que pour n=k²+k-1 Vn+V(n+1)<2k+1=2V(k²+k+1/4)
Ici, la lecture directe le prouve.
V(k²+k-1)+V(k²+k)<2V(k²+k+1/4).
C'est donc OK aussi pour un carré impair.
24 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 15 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
