Bonjour!
Je suis un nouveau membre sur ce forum, 18 ans, passioné des maths, en 4ème au Collège (Suisse) donc sauf erreur Lycée en France.
En fait j'aimerais savoir si quelqu'un a une réponse au problème suivant. Lorsqu'on utiliser le théorème de Taylor pour trouver la série de Taylor d'une quelconque fonction f, suivant la fonction, on obtient une série qui converge vers la valeur cherché (f(x)), ou qui diverge. Si le reste de Laplace est infiniment petit pour un nombre de termes n infiniment grand dans la série de Taylor, alors la série converge. Ma question est: est-ce qu'il existe un critère qui permette de dire sans difficulté pour une quelconque fonction f si la série de Taylor converge vers f(x) sans avoir à refaire tout le travail à partir du reste de Laplace pour savoir s'il est ou non infiniment petit pour un n infiniment grand ?
Ou, est-ce que quelqu'un sait à qui dois-je m'adresser pour avoir une réponse à ce problème ? En fait j'ai cherché sur Internet et je n'ai rien trouvé. Si un tel critère existait, ce serait très utile, car un grand travail serait épargné à l'heure de démontrer que par exemple sin, cos, exp... sont des fonctions dont on peut trouver l'image pour tout x en utilisant la série de Taylor, et cela en vérifiant un simple critère général.
Reste de Laplace (Théorème de Taylor)
4 messages
- Page 1 sur 1
Bonjour,
Aguila, si un tel critere existait, et s'il etait aussi simple d'application que tu le souhaites, ca se saurait !
!
Maintenant, pour tes exemples exp, sin, cos..., tu te fatigues peut etre maintenant pour montrer que ce "sont des fonctions dont on peut trouver l'image pour tout x en utilisant la série de Taylor", mais lorsque tu auras quelques annees de vol supplementaires, tu verras que c'est en fait plus "simple" que cela !
En fait, ces fonctions, si tu les consideres comme des fonctions de C dans C, sont ce qu'on appelle des fonctions holomorphes. Et une propriete extremement interessantes de ces betes la, c'est qu'elles sont toujours somme de leur serie de Taylor (mais pas forcement sur C tout entier).
Je te conseille donc de te renseigner sur ces fonctions holomorphes... Mais quoi qu'il en soit, a ton niveau (il n'y a rien de meprisant dans ma phrase !!!), il n'y a pas de recette de cuisine pour montrer qu'une fonction est somme de sa serie de Taylor !
Roman
Aguila, si un tel critere existait, et s'il etait aussi simple d'application que tu le souhaites, ca se saurait
Maintenant, pour tes exemples exp, sin, cos..., tu te fatigues peut etre maintenant pour montrer que ce "sont des fonctions dont on peut trouver l'image pour tout x en utilisant la série de Taylor", mais lorsque tu auras quelques annees de vol supplementaires, tu verras que c'est en fait plus "simple" que cela !
En fait, ces fonctions, si tu les consideres comme des fonctions de C dans C, sont ce qu'on appelle des fonctions holomorphes. Et une propriete extremement interessantes de ces betes la, c'est qu'elles sont toujours somme de leur serie de Taylor (mais pas forcement sur C tout entier).
Je te conseille donc de te renseigner sur ces fonctions holomorphes... Mais quoi qu'il en soit, a ton niveau (il n'y a rien de meprisant dans ma phrase !!!), il n'y a pas de recette de cuisine pour montrer qu'une fonction est somme de sa serie de Taylor !
Roman
Bonjour,
C'est plus compliqué que ça en fait : on peut avoir une série de Taylor qui converge, mais pas vers f ! Il y a des fonctions de série de Taylor nulle en un point qui ne sont pas nulles au voisinage de ce point, par exemple la fonction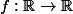 définie par
définie par  = e^{\frac{-1}{x^2}}) si
si 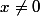 et
et  = 0) . On montre (à la main, par récurrence) que c'est une fonction de classe
. On montre (à la main, par récurrence) que c'est une fonction de classe  sur
sur  et que ses dérivées successives en 0 sont nulles, donc la série de Taylor de f en 0 est nulle, mais f n'est pas nulle au voisinage de 0.
et que ses dérivées successives en 0 sont nulles, donc la série de Taylor de f en 0 est nulle, mais f n'est pas nulle au voisinage de 0.
Sinon Roman t'a déjà répondu, il n'y a pas de critère génarél pour la convergence.
Aguila a écrit:En fait j'aimerais savoir si quelqu'un a une réponse au problème suivant. Lorsqu'on utiliser le théorème de Taylor pour trouver la série de Taylor d'une quelconque fonction f, suivant la fonction, on obtient une série qui converge vers la valeur cherché (f(x)), ou qui diverge.
C'est plus compliqué que ça en fait : on peut avoir une série de Taylor qui converge, mais pas vers f ! Il y a des fonctions de série de Taylor nulle en un point qui ne sont pas nulles au voisinage de ce point, par exemple la fonction
Sinon Roman t'a déjà répondu, il n'y a pas de critère génarél pour la convergence.
Merci! En fait, si j'ai bien compris, toute fonction holomorphe est somme de sa série de Taylor... et donc je vais me renseigner sur ce qu'est une fonction holomorphe, mais j'ai comme l'impression que c'est le critère que je cherchais. Si je peux dire: "une fonction f est holomorphe, donc sa série de Taylor converge vers f(x)", alors j'ai trouvé ce que je cherchais.
En fait je ne cherche pas un truc de cuisine, alors pas du tout. Il se trouve seulement qu'à mon niveau je ne dispose pas de tous les outils nécessaires pour vérifier rigoureusement tout ce que je fais, et que justement ce critère que je cherchais j'ai l'impression de l'avoir trouvé, après une démonstration qui m'a pris pas mal de temps. Ce que je veux savoir c'est si ma démonstration est juste, et je pense bien que si c'est le cas je ne suis pas le premier à l'avoir trouvée, et donc je peux sans doute la retrouver sur Internet, ce qui confirmerait (ou pas) que je n'ai pas fait tout ce travail pour rien. Mon prof de maths à priori pense que c'est juste (c'est pas dans le cadre du cours, lui normalement il démontre indépendament pour sin, cos, exp...). Avec ma démonstration, si elle marche, alors on démontre d'un coup et très facilement pour ces trois donctions que leur série de Taylor tend bien vers f(x).
Je vais cependant voir encore ce qu'est une fonction holomorphe. Si ça se trouve mon critère cherché correspond à la définition de la fonction holomorphe ou à une partie de la définition... Merci encore!!!
Si j'ai le temps je transcris la démonstration sur ordinateur et comme ça vous pourriez la vérifier.
En fait je ne cherche pas un truc de cuisine, alors pas du tout. Il se trouve seulement qu'à mon niveau je ne dispose pas de tous les outils nécessaires pour vérifier rigoureusement tout ce que je fais, et que justement ce critère que je cherchais j'ai l'impression de l'avoir trouvé, après une démonstration qui m'a pris pas mal de temps. Ce que je veux savoir c'est si ma démonstration est juste, et je pense bien que si c'est le cas je ne suis pas le premier à l'avoir trouvée, et donc je peux sans doute la retrouver sur Internet, ce qui confirmerait (ou pas) que je n'ai pas fait tout ce travail pour rien. Mon prof de maths à priori pense que c'est juste (c'est pas dans le cadre du cours, lui normalement il démontre indépendament pour sin, cos, exp...). Avec ma démonstration, si elle marche, alors on démontre d'un coup et très facilement pour ces trois donctions que leur série de Taylor tend bien vers f(x).
Je vais cependant voir encore ce qu'est une fonction holomorphe. Si ça se trouve mon critère cherché correspond à la définition de la fonction holomorphe ou à une partie de la définition... Merci encore!!!
Si j'ai le temps je transcris la démonstration sur ordinateur et comme ça vous pourriez la vérifier.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 11 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
