Endomorphisme nilpotent

[Sheeppowa]

Bonjour tout le monde, voici un exercice que j'essaie de régler.

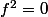
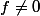
Soit E un K-espace vectoriel de dimension 3, et telle que et ; Montrer que

Donc déjà on a , donc cela suppose a montrer que .

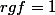
De plus étant donné que f est nilpotent on a :



Don rgf = rg .

Mais ce rang dépend des valeurs de .

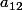
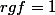
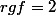
Si est nul alors , de même si est nul mais si est nul alors et donc ça ne marche, ce qui me dérange c'est que dans l'énoncé, ce n'est pas précisé de montrer le résultat suivant les valeurs des indices dans la matrice.

[jlb]

cela te dit quoi f²=0 en terme de noyau et image?

si y=f(x) alors f(y)=???

[Sheeppowa]

cela te dit quoi f²=0 en terme de noyau et image?

si y=f(x) alors f(y)=???

Et bien f(y) = 0, d’où y appartient a Ker (f)

[Maxmau]

Bonjour tout le monde, voici un exercice que j'essaie de régler.

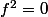
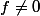
Soit E un K-espace vectoriel de dimension 3, et telle que et ; Montrer que

Donc déjà on a , donc cela suppose a montrer que .

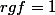
De plus étant donné que f est nilpotent on a :



Don rgf = rg .

Mais ce rang dépend des valeurs de .

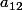
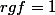
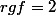
Si est nul alors , de même si est nul mais si est nul alors et donc ça ne marche, ce qui me dérange c'est que dans l'énoncé, ce n'est pas précisé de montrer le résultat suivant les valeurs des indices dans la matrice.

Bj
Ecris que le carré de ta matrice est une matrice nulle (puisque f² = 0)

[jlb]

Et bien f(y) = 0, d’où y appartient a Ker (f)

donc Imf C Kerf ce qui se traduit sur les dimensions par?

[Sheeppowa]

Bj
Ecris que le carré de ta matrice est une matrice nulle (puisque f² = 0)

Et bien si on appelle A la matrice de u dans la base B on a :



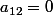
D'ou ou/et

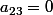
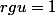
Donc ( pardon j'ai mélangé u et f dans mon tout premier message mais ce sont les mêmes )

[Sheeppowa]

donc Imf C Kerf ce qui se traduit sur les dimensions par?

Ah oui exact j'avais pas vu comme ça.

Donc on a or , de plus car il contient y, D'ou et