Équation difficile avec ln
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 11 Déc 2013, 00:51
par Jimm15 » 11 Déc 2013, 00:51
Bonjour,
Je bloque sur cette équation, la racine m'embête :
+3\ln(\sqrt{x-1})=\ln{8})
.
J'en suis arrivé à :
(x-1)\sqrt{x-1}=8)
Et je ne vois pas comment continuer...
Merci d'avance.

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 11 Déc 2013, 01:08
par Lostounet » 11 Déc 2013, 01:08
Jimm15 a écrit:Bonjour,
Je bloque sur cette équation, la racine m'embête :
+3\ln(\sqrt{x-1})=\ln{8})
.
J'en suis arrivé à :
(x-1)\sqrt{x-1}=8)
Et je ne vois pas comment continuer...
Merci d'avance.
Salut,
Un moyen de trouver une solution... On sait que 8 c'est 2 * 4, donc on remarque que si x = 5
1*4*;)4 = 4*2 = 8, l'égalité est vérifiée.
Ensuite, on peut étudier les variations de la fonction f définie par f(x) = (x - 4)(x - 1);)(x - 1) - 8 et de montrer que x = 5 est la seule solution (théorème des valeurs intermédiaires?)
Il y a peut-être une méthode plus adaptée.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.

-
ortollj
- Membre Rationnel
- Messages: 554
- Enregistré le: 13 Mai 2009, 08:28
-
 par ortollj » 11 Déc 2013, 04:52
par ortollj » 11 Déc 2013, 04:52
Bonjour
f(x)=ln(x-4)+ 3 ln(sqrt(x-1)) - ln(8)=0
ln(a.b)=ln(a) +ln(b) et ln(a/b)=ln(a) - ln(b) et ln (a^b)=b ln(a)
f(x)=ln((x-4)/8) + ln( (x-1)^(3/2) )=0
f(x)=ln(((x-4)/8) ( (x-1)^(3/2) ) )=0
((x-4)/8) ( (x-1)^(3/2) ) - 1 = 0
mais moi non plus je ne sais pas resoudre cette equation :triste:
si j'avais su j'aurais pas venu.
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 11 Déc 2013, 09:42
par Jimm15 » 11 Déc 2013, 09:42
Merci pour vos réponses.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 11 Déc 2013, 13:28
par Ben314 » 11 Déc 2013, 13:28
Salut,
Partant de
(x-1)\sqrt{x-1}=8)
, on peut evidement tout élever au carré (pour enlever la racine) en gardant à l'esprit que le terme de gauche doit être positif : on obtient un polynôme de degrè 5 et il faut... bruler un cierge pour espérer qu'il ait pas mal de "racines évidentes" pour pouvoir le factoriser.
On peut aussi poser

(donc
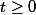
) d'où

et l'équation devient
t^3=8)
qui est aussi de degrè 5 (mais un peu plus simple et plus rapide à obtenir)
Aprés avoir "vu" la racine évidente
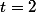
on obtient
 (t^4+2 t^3+t^2+2 t+4)=0)
et, comme t doit être positif, il est clair que la seule solution est
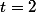
, c'est à dire
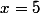
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 11 Déc 2013, 14:39
par Jimm15 » 11 Déc 2013, 14:39
Merci Ben314, votre solution est très intéressante.

-
ortollj
- Membre Rationnel
- Messages: 554
- Enregistré le: 13 Mai 2009, 08:28
-
 par ortollj » 11 Déc 2013, 18:10
par ortollj » 11 Déc 2013, 18:10
Jimm15 a écrit:Bonjour,
Je bloque sur cette équation, la racine m'embête :
+3\ln(\sqrt{x-1})=\ln{8})
.
J'en suis arrivé à :
(x-1)\sqrt{x-1}=8)
Et je ne vois pas comment continuer...
Merci d'avance.
comment de
+3\ln(\sqrt{x-1})=\ln{8})
.
arrives tu a
(x-1)\sqrt{x-1}=8)
? :doh:
moi je trouve
 \text{ } (x-1)^{\frac{3}{2}}\text{ } ) - 1 = 0)
peut etre je n'avais pas compris ce sont 2 exercices différents ?
ou peut etre me suis je trompé ?
si j'avais su j'aurais pas venu.

-
ortollj
- Membre Rationnel
- Messages: 554
- Enregistré le: 13 Mai 2009, 08:28
-
 par ortollj » 11 Déc 2013, 18:13
par ortollj » 11 Déc 2013, 18:13
ortollj a écrit:comment de
+3\ln(\sqrt{x-1})=\ln{8})
.
arrives tu a
(x-1)\sqrt{x-1}=8)
? :doh:
moi je trouve
 \text{ } (x-1)^{\frac{3}{2}}\text{ } ) - 1 = 0)
peut etre je n'avais pas compris ce sont 2 exercices différents ?
ou peut etre me suis je trompé ?
oups pardon , j'ai pedalé dans la semoule ! :hum:
si j'avais su j'aurais pas venu.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 85 invités
.
.