Problème avec la continuité de x²y²/(x²+y²)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
irfaan03
- Messages: 3
- Enregistré le: 07 Déc 2013, 12:36
-
 par irfaan03 » 07 Déc 2013, 12:46
par irfaan03 » 07 Déc 2013, 12:46
Bonjour,
Alors voila , j'ai un souci et je bloque un peu avec la limite en 0 des fonctions à deux variables.
En fait j'ai une fonction f(x) = x²y²/(x²+y²) et la question est la suivante;
Montrer que la fonction est continue sur R²\{0,0} puis étudier le problème de prolongement en (0,0)
je sais qu'on peut passer en coordonnées polaires pour trouver la limite en (0,0) mais je ne comprend pas comment dire que la fonction est continue sur R²\(0,0)
Merci beaucoup..

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 07 Déc 2013, 13:04
par Ben314 » 07 Déc 2013, 13:04
Salut,
Effectivement, ici, le plus simple est sans doute les coordonnées polaires.
Si tu prend
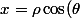)
et
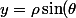)
, ça te permet de montrer que
\leq \rho^2)
ce qui montre que f(x,y) tend vers 0 lorsque

tend vers 0
indépendamment de 
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Archibald
- Membre Relatif
- Messages: 415
- Enregistré le: 05 Avr 2013, 17:06
-
 par Archibald » 07 Déc 2013, 13:57
par Archibald » 07 Déc 2013, 13:57
Bonjour,
problème assez classique. Il suffit de remarquer que :

donc que

maintenant que ta fonction est encadrée, tu peux passer aux limites et conclure par le théorème des gendarmes.
édit : on pourrait aussi s'approcher de l'origine selon une parabole
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 07 Déc 2013, 15:53
par Joker62 » 07 Déc 2013, 15:53
Pour répondre à la vraie question :
La continuité sur R^2\{(0,0)} c'est juste parce que c'est une fraction rationnelle en x et y.
Elle est donc continue là où elle est définie.
-
irfaan03
- Messages: 3
- Enregistré le: 07 Déc 2013, 12:36
-
 par irfaan03 » 07 Déc 2013, 17:39
par irfaan03 » 07 Déc 2013, 17:39
SUPER ! MERCI BEAUCOUP :)
Donc on peut aussi dire que x²+y² ;) x²
et donc 1/ x²+y² ;) 1/x² => x²y²/x²+y² ;) x²y²/x² => x²y²/x²+y² ;) y²
et conclure que la limite = 0 n'est ce pas?
En tout cas merci beaucoup :)
-
Archibald
- Membre Relatif
- Messages: 415
- Enregistré le: 05 Avr 2013, 17:06
-
 par Archibald » 07 Déc 2013, 18:03
par Archibald » 07 Déc 2013, 18:03
Non, on ne peut pas conclure de cette façon.
Le théorème des gendarmes c'est un encadrement, ici, rien ne nous permet de dire que
\to (0,0)} f(x,y) = 0)
Tu sais juste qu'elle est
inférieure ou égale à 0, nuance.
D'où l'utilisation de la valeur absolue pour encadrer ta fonction. Tu sais comment l'utiliser, n'est-ce pas ?
-
irfaan03
- Messages: 3
- Enregistré le: 07 Déc 2013, 12:36
-
 par irfaan03 » 07 Déc 2013, 18:12
par irfaan03 » 07 Déc 2013, 18:12
Archibald a écrit:Non, on ne peut pas conclure de cette façon.
Le théorème des gendarmes c'est un encadrement, ici, rien ne nous permet de dire que
\to (0,0)} f(x,y) = 0)
Tu sais juste qu'elle est
inférieure ou égale à 0, nuance.
D'où l'utilisation de la valeur absolue pour encadrer ta fonction. Tu sais comment l'utiliser, n'est-ce pas ?
Oui j'ai une idée mais tu peux me l'expliquer quand même?
Merci


-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 07 Déc 2013, 19:22
par Ben314 » 07 Déc 2013, 19:22
Archibald a écrit:...Tu sais juste qu'elle est inférieure ou égale à 0, nuance.
Là, tu chipote un peu : Sur le principe théorique, O.K., mais là, la fonction est clairement positive...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Archibald
- Membre Relatif
- Messages: 415
- Enregistré le: 05 Avr 2013, 17:06
-
 par Archibald » 08 Déc 2013, 16:14
par Archibald » 08 Déc 2013, 16:14
Quand j'écrivais mon poste, j'avais en tête xy² au numérateur... ceci explique cela.
@irfaan03 :
 \| \ \leq \ x^2 \ \Longleftrightarrow \ -x^2 \ \leq \ f(x,y) \ \leq \ x^2)
mais ici tu n'en a pas besoin car la fonction est positive sur tout R².
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
