Diagonalisation avec des espaces propres
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
 par ThekamikazeFou » 07 Déc 2013, 15:03
par ThekamikazeFou » 07 Déc 2013, 15:03
Bonjour,
voila j'ai une matrice généralisé 2x2 de ce type :

je cherche à la diagonalisé en utilisant des valeurs propres.
je trouve deux valeurs propres p et q avec p<q
j'effectues un resonnement sur les deux espaces propres pour en connaitre leurs base. puis j'en déduis une matrice de passage P
pour finir, j'ai la matrice A diagonalisé qui vaut

est il utile d'effectuer tout un raisonnement avec la matrice de passe pour trouver la matrice diagonalisée?
c'est à dire une fois avoir trouver p et q, ne pouvons nous pas écrire directement la matrice de diagonalisée?
merci

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 07 Déc 2013, 15:10
par Ben314 » 07 Déc 2013, 15:10
Salut,
Ca dépend de ce qu'on te demande ensuite de faire avec la matrice A.
Si la question est uniquement "peut on la diagonaliser et quelle sera la matrice diagonale obtenue", tu n'a pas besoin de calculer P (ni P^(-1))
Si on te demande par exemple d'exprimer A^n en fonction de n, ça risque d'être un peu plus difficile si tu ne calcule pas P et P^(-1)
P.S. Faire aussi attention à ce que toutes les matrices 2x2 ne sont pas diagonalisable, même dans le corps des complexes.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
 par ThekamikazeFou » 07 Déc 2013, 15:14
par ThekamikazeFou » 07 Déc 2013, 15:14
donc merci je voulais juste savoir si pour une matrice 2x2 avec comme spectre(p,q)
la formule générale de la diagonalisation etait toujours :

visiblement oui.
par contre, comment savoir si la matrice n'est pas :

mais

?
derniere question, cette "formule" ce généralise telle pour des matrices nxn ?
c'est à dire si j'ai un spectre B (n,p,q,r) alors la diagonalisation de B vaut :


-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 07 Déc 2013, 15:17
par Ben314 » 07 Déc 2013, 15:17
ThekamikazeFou a écrit:
mais

Vu le contexte, ça ne change rien : ça va dépendre de l'ordre dans lequel tu met tes vecteurs propres dans la matrice P :
Si tu met celui correspondant à p en première colonne tu obtient la matrice diagonale avec un p sur la première colonne.
De même dans l'autre sens si tu commence par prendre comme première colonne de P un vecteur propre correspondant à q ta matrice diagonale "commencera" par q.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 07 Déc 2013, 15:22
par Ben314 » 07 Déc 2013, 15:22
ThekamikazeFou a écrit:c'est à dire si j'ai un spectre B (n,p,q,r) alors la diagonalisation de B vaut :

tout à fait,
à condition que n,p,q et r soient distincts.
Lorsque tu n'a que 3 valeurs propres pour une matrice 4x4, elle peut être diagonalisable... ou ne pas l'être...
Ca va dépendre de la dimension des sous espaces propres associés à tes valeurs propres : si la somme des dimensions fait 4 (par exemple 1+2+1), c'est bon.
Sinon (1+1+1), c'est pas bon...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
 par ThekamikazeFou » 07 Déc 2013, 15:22
par ThekamikazeFou » 07 Déc 2013, 15:22
parce que spectA(p,q) != spect(q,p) ?
je ne savais pas.
ok merci pour la généralisation, le concept de sous espace propre est encore assez flou.
merci !

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 07 Déc 2013, 15:26
par Ben314 » 07 Déc 2013, 15:26
Pour moi, en dimension finie, le spectre d'une matrice (ou d'un endomorphisme), c'est l'ensemble des valeurs propres.
Et dans un ensemble, (contrairement à un n-uplet), l'ordre des éléments n'a pas d'importance : {0,1}={1,0} est l'ensemble contenant les réels 0 et 1 (souvent, on préfère les écrire du plus petit au plus grand dans le cas des réels, mais ce n'est pas une obligation et en plus, ça n'a plus de sens dans le cas où c'est des complexes ou des points du plan par exemple)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
 par ThekamikazeFou » 07 Déc 2013, 15:32
par ThekamikazeFou » 07 Déc 2013, 15:32
ok je comprends ce que vous voulez dire, mais pourquoi si spectA(p,q) on ne peut pas dire que la diagonalisation de A est

alors que spectA(p,q) spectA(q,p ) ?
sinon merci j'ai bien compris la généralisation nxn avec la somme des dimensions :lol3:
ça me parait évident maintenant!

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 07 Déc 2013, 15:33
par Ben314 » 07 Déc 2013, 15:33
ThekamikazeFou a écrit:...le concept de sous espace propre est encore assez flou...
J'ai utilisé ce terme parce que c'est celui que tu as utilisé dans ton premier post.
Dire que p est une valeur propre de la matrice A (nxn), ça veut dire qu'il existe un vecteur colonne X (nx1)
non nul tel que AX=pX.
Après, le sous espace propre associé à la valeur propre p, c'est tout simplement l'ensemble des vecteurs X tels que AX=pX.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 07 Déc 2013, 15:37
par Ben314 » 07 Déc 2013, 15:37
Concernant la façon d'écrire les choses, je sais que perso, je n'écrirais pas "spectA(p,q)", mais plutôt un truc du style "Spec(A)={p,q}" : Le spectre de la matrice A est l'ensemble {p,q}
Ce qui signifie que les valeurs propres de A sont p et q (dans un ordre totalement indifférencié)
Tient, pour te faire faire un petit calcul, si on prend
)
et
)
, c'est qui
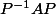
?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
 par ThekamikazeFou » 07 Déc 2013, 15:38
par ThekamikazeFou » 07 Déc 2013, 15:38
Ok merci beaucoup Ben314 !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
