Cissoïde de Dioclès
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
vince_57
- Membre Relatif
- Messages: 163
- Enregistré le: 23 Nov 2011, 21:06
-
 par vince_57 » 02 Déc 2013, 22:28
par vince_57 » 02 Déc 2013, 22:28
Bonjour j'ai du mal avec l'exercice suivant:
Soit f la fonction définie par f(x)= racine de( x^3/1-x) sur [0;1[.
1)a) Calculer f(0);f(1/2) et lim x->1 f(x) (interpréter le résultat).
b)Dresser le tableau des variations de f sur [0;1[. Détailler et justifier toutes les étapes.
Ce que j'ai trouvé:
1)a) f(0)=0 ; f(1/2)=racine de (1/8 / 1/2) et lim de f = +oo
b) pour 0 f=0 et pour 1 f=+oo en étant croissant mais je ne sais pas vraiment comment faire :hum:
Merci d'avance
-
vince_57
- Membre Relatif
- Messages: 163
- Enregistré le: 23 Nov 2011, 21:06
-
 par vince_57 » 03 Déc 2013, 11:18
par vince_57 » 03 Déc 2013, 11:18
quelqu'un ?
-
coqp-ox
- Membre Naturel
- Messages: 52
- Enregistré le: 22 Nov 2013, 09:00
-
 par coqp-ox » 03 Déc 2013, 11:30
par coqp-ox » 03 Déc 2013, 11:30
Si vous avez commencé à étudier les dérivées alors il suffit de dériver
)
puis de regarder son signe sur [0,1[
Et évidemment, en fonction de ce que tu trouves tu obtiens ton tableau de variations
-
vince_57
- Membre Relatif
- Messages: 163
- Enregistré le: 23 Nov 2011, 21:06
-
 par vince_57 » 03 Déc 2013, 15:30
par vince_57 » 03 Déc 2013, 15:30
la dérivé de x^3=3x² et 1-x=x donc la dérivée de la fonction f est : 1/2*racine carré de (3x) ???
-
coqp-ox
- Membre Naturel
- Messages: 52
- Enregistré le: 22 Nov 2013, 09:00
-
 par coqp-ox » 03 Déc 2013, 16:09
par coqp-ox » 03 Déc 2013, 16:09
La première oui, mais pour
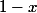
, on obtient -

Ensuite ca ne suffit pas,
'=w'/2sqrt(w))
Or ici,
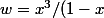)
Comme on peut le voir

et
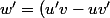/v^2)
-
vince_57
- Membre Relatif
- Messages: 163
- Enregistré le: 23 Nov 2011, 21:06
-
 par vince_57 » 05 Déc 2013, 10:48
par vince_57 » 05 Déc 2013, 10:48
donc f'(x) = 2
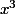
-3 / 2
})
????
-
coqp-ox
- Membre Naturel
- Messages: 52
- Enregistré le: 22 Nov 2013, 09:00
-
 par coqp-ox » 05 Déc 2013, 10:59
par coqp-ox » 05 Déc 2013, 10:59
vince_57 a écrit:donc f'(x) = 2
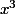
-3 / 2
})
????
Voila ce que je trouve :
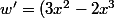/(1-x)^2)
De la tu calcule ton
' = f'(x))
Et ensuite, normalement, tu peux facilement déduire que le signe de
)
dépend juste de

Tu n'as donc plus qu'à compléter ton tableau de variations :ptdr:
-
vince_57
- Membre Relatif
- Messages: 163
- Enregistré le: 23 Nov 2011, 21:06
-
 par vince_57 » 05 Déc 2013, 11:53
par vince_57 » 05 Déc 2013, 11:53
mais w' au numérateur donne (3x²*(1-x)) - (x^3*(-x)) ce qui est égale à 3x²-3x^3+x^4 non ?
-
coqp-ox
- Membre Naturel
- Messages: 52
- Enregistré le: 22 Nov 2013, 09:00
-
 par coqp-ox » 05 Déc 2013, 12:05
par coqp-ox » 05 Déc 2013, 12:05
vince_57 a écrit:mais w' au numérateur donne (3x²*(1-x)) - (x^3*(-x)) ce qui est égale à 3x²-3x^3+x^4 non ?
Tu as refais la même erreur
'=-1)
c'est tout ^^
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
