[TES] Problème pour trouver la dérivée
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 04 Déc 2013, 16:31
par Carpate » 04 Déc 2013, 16:31
Et la question 1 est ...
-
titinouille
- Membre Relatif
- Messages: 169
- Enregistré le: 15 Mar 2010, 17:47
-
 par titinouille » 04 Déc 2013, 16:32
par titinouille » 04 Déc 2013, 16:32
Carpate a écrit:Et la question 1 est ...
Désolé, la photo ne s'affiche pas. J'ai mis le lien de la photo hébergée, j'espère que c'est bon.
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 04 Déc 2013, 16:39
par Carpate » 04 Déc 2013, 16:39
OK donc le problème est de dériver

Applique
}{v(x)})'=\frac{v(x)u'(x)-u(x)v'(x)}{v(x)^2})
avec
=15x^3-120x^2+500x+750)
et
=x)
et donne ton résultat ...
-
titinouille
- Membre Relatif
- Messages: 169
- Enregistré le: 15 Mar 2010, 17:47
-
 par titinouille » 04 Déc 2013, 17:15
par titinouille » 04 Déc 2013, 17:15
Je trouve
(-15x^4 +120x^3 +545x^2 +510x +500)/x^2
Désolé pour l'écriture, je suis sur mobile
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 04 Déc 2013, 17:45
par Carpate » 04 Déc 2013, 17:45
titinouille a écrit:Je trouve
(-15x^4 +120x^3 +545x^2 +510x +500)/x^2
Désolé pour l'écriture, je suis sur mobile
Il ny a pas de terme en
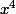
=\frac{x(45x^2-240x+500)-(15x^3-120x^2+500x+750)}{x^2}=\frac{30(x^3-4x^2-25)}{x^2})
Et comme on te le suggère

est divisible par
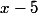
-
titinouille
- Membre Relatif
- Messages: 169
- Enregistré le: 15 Mar 2010, 17:47
-
 par titinouille » 04 Déc 2013, 17:56
par titinouille » 04 Déc 2013, 17:56
Carpate a écrit:Il ny a pas de terme en
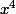
=\frac{x(45x^2-240x+500)-(15x^3-120x^2+500x+750)}{x^2}=\frac{30(x^3-4x^2-25)}{x^2})
Et comme on te le suggère

est divisible par
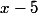
Oui je trouvais cela bizarre. Merci, grâce à toi j'ai vu où était mon erreur de calcul.
Par contre je ne comprend pas cette histoire de (x-5)
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 04 Déc 2013, 18:15
par Carpate » 04 Déc 2013, 18:15
titinouille a écrit:Oui je trouvais cela bizarre. Merci, grâce à toi j'ai vu où était mon erreur de calcul.
Par contre je ne comprend pas cette histoire de (x-5)
Si tu remplace x par 5 dans x^3-4x^2-25, tu trouves 0 donc x^3-4x^2-25 est divisible par 5

=
)
(trinôme du second degré)
l'énoncé t'indique que le numérateur est
(x^2+x+5))
Tu peux vérifier que
(x^2+x+5)=x^3-4x^2-25)
-
titinouille
- Membre Relatif
- Messages: 169
- Enregistré le: 15 Mar 2010, 17:47
-
 par titinouille » 04 Déc 2013, 18:31
par titinouille » 04 Déc 2013, 18:31
Carpate a écrit:Si tu remplace x par 5 dans x^3-4x^2-25, tu trouves 0 donc x^3-4x^2-25 est divisible par 5

=
)
(trinôme du second degré)
l'énoncé t'indique que le numérateur est
(x^2+x+5))
Tu peux vérifier que
(x^2+x+5)=x^3-4x^2-25)
Tout est clair maintenant, merci de ton aide

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 93 invités
