Dérivée partielles quotient
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
rb90
- Membre Naturel
- Messages: 65
- Enregistré le: 25 Mai 2012, 13:07
-
 par rb90 » 02 Déc 2013, 01:30
par rb90 » 02 Déc 2013, 01:30
Bonsoir
Je cherche la dérivée partielle de cette exercice
http://imageshack.us/photo/my-images/43/o1hg.jpg/Pour la dérivée partiel de x
je trouve
^2})
A priori j'ai faux je ne comprend pas pourquoi !!!
J'ai tout mis au meme numérateur pour avoir une forme u'u ensuite j'ai multiplié

avec
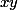
pour dériver par rapport à x
Ma prof ma dit que la réponse était
^2})
Mais je ne sais pas d'ou elle sort son -yx^2
-
frankyboy1994
- Membre Naturel
- Messages: 37
- Enregistré le: 31 Oct 2013, 17:45
-
 par frankyboy1994 » 02 Déc 2013, 02:46
par frankyboy1994 » 02 Déc 2013, 02:46
fx=(;)(xy)/;)x (x^2+y^2-2y-3)-;)(x^2+y^2-2y-3)/;)x (xy))/(;)(x;)^2+y^2-2y-3)²)=(y(x^2+y^2-2y-3)-2x(xy))/(;)(x;)^2+y^2-2y-3)²)=(x^2 y+y^3-2y^2-3y-2x^2 y)/(;)(x;)^2+y^2-2y-3)²)=(y^3-2y^2-3y-x^2 y)/((x^2+y^2-2y-3)²)
-
rb90
- Membre Naturel
- Messages: 65
- Enregistré le: 25 Mai 2012, 13:07
-
 par rb90 » 02 Déc 2013, 12:48
par rb90 » 02 Déc 2013, 12:48
Merci j'ai compris
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 02 Déc 2013, 12:51
par Sylviel » 02 Déc 2013, 12:51
Je ne comprends pas le message de Franky.
Pour rb90 : imagines que y sont des constantes (remplace y par pi si cela t'aide) et dérive la fonction selon la formule habitulle (u/v)' = (u'v-uv')/v²
EDIT : :marteau: c'était pour vérifier que le lecteur suivait bien :zen:
Merci Ben de veiller au grain.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
rb90
- Membre Naturel
- Messages: 65
- Enregistré le: 25 Mai 2012, 13:07
-
 par rb90 » 02 Déc 2013, 13:06
par rb90 » 02 Déc 2013, 13:06
Merci pour la réponse, je viens de me rendre compte que c'est de la forme (u/v)' = (u'v-uv')/u²

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 02 Déc 2013, 13:07
par Ben314 » 02 Déc 2013, 13:07
Sylviel a écrit:... formule habitulle (u/v)' = (u'v-uv')/u²
...petite faute de frappe...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
