Limite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Gonra
- Membre Relatif
- Messages: 100
- Enregistré le: 06 Déc 2012, 21:34
-
 par Gonra » 01 Déc 2013, 18:34
par Gonra » 01 Déc 2013, 18:34
Bonsoir ,
je n'arrive pas à trouver la limite de
-xln(x+2))
sans passer par changement variable puis la règle de l'hopital qui sont Hors programme si quelquun a une piste ,
Merci d'avance pour votre aide
-
kangourex
- Membre Naturel
- Messages: 32
- Enregistré le: 21 Nov 2013, 18:39
-
 par kangourex » 01 Déc 2013, 18:36
par kangourex » 01 Déc 2013, 18:36
(Lim x * Lim ln(x)) -( Lim x * Lim(x+2)) si ça fait -infini - (-infini) faut factoriser pour savoir lequel est le plus grand
-
Gonra
- Membre Relatif
- Messages: 100
- Enregistré le: 06 Déc 2012, 21:34
-
 par Gonra » 01 Déc 2013, 18:41
par Gonra » 01 Déc 2013, 18:41
J'ai essayé toute les factorisations avec le Ln
c'est censée tendre vers -2
-
kangourex
- Membre Naturel
- Messages: 32
- Enregistré le: 21 Nov 2013, 18:39
-
 par kangourex » 01 Déc 2013, 18:45
par kangourex » 01 Déc 2013, 18:45
Oui C'est bien cela. Il est très simple de vérifier, avec une calculette graphique. :zen:
-
Gonra
- Membre Relatif
- Messages: 100
- Enregistré le: 06 Déc 2012, 21:34
-
 par Gonra » 01 Déc 2013, 19:02
par Gonra » 01 Déc 2013, 19:02
voila mon raisonnement :
x(ln(x)-ln(x+2))
Posons x=(1/t)
si x tend vers +

t tend vers 0
-ln((1/t)+2)}{t})
il y a une indéterminé 0/0
donc la règle de l'hopital est utilisable :
en dérivant le haut et le bas selon t:
sa fait

qui tend vers -2
mais je vois pas autrement ......

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 01 Déc 2013, 19:10
par chan79 » 01 Déc 2013, 19:10
essaie avec
-ln(x+2))=-x(ln(1+\fra{2}{x}))=-2\fra{ln(1+\fra{2}{x})}{\fra{2}{x}})
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 01 Déc 2013, 19:12
par jlb » 01 Déc 2013, 19:12
x(lnx-ln(x+2))=xln(x/(x+2))=-xln((x+2)/x)=-xln(1+2/x)=-2 ln(1+2/x) / (2/x)
après lim (u tend vers 0) ln(1+u)/u= (ln)'(1)=1 c'est la définition de la dérivée de ln en 1
-
Gonra
- Membre Relatif
- Messages: 100
- Enregistré le: 06 Déc 2012, 21:34
-
 par Gonra » 01 Déc 2013, 19:16
par Gonra » 01 Déc 2013, 19:16
Merci pour votre aide Chan79 bonne soirée.
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 06 Déc 2013, 15:29
par deltab » 06 Déc 2013, 15:29
Bonjour.
Si la règle de l'Hôpital ne peut être utilisée, rien n'interdit de la contourner c.à.d. faire apparaitre dans l'expression donnée directement ou après changement de variable un ou plusieurs taux d'accroissement dont la limite est bien une dérivée. C'est ce qu'a fait Chan79 quand il est arrivé à
-x\ln(x+2)=-2 \dfrac{\ln(1+\dfrac{2}{x})}{\dfrac{2}{x}})
. En posant

, l'expression
}{\dfrac{2}{x}})
est bien de la forme
-f(t_0)}{t-t_0})
avec
=\ln(1+t))
et
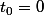
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités