Bonjour,
Soit f: I-->J
x-->xe^x
f est elle bijective pour : a) I=J=R b) I=J=[1;+oo[ c) I=J=[0;+oo[
J'ai résolu l'exercice en faisant un tableau de variation mais j'aimerais avoir une autre méthode, plus démonstrative sans s'appuyer sur un tableau.
Pouvez vous m'expliquer cette deuxième méthode ?
merci
NB: avec le tableau, je trouve que : a) surjective b) bijective c) bijective
Application
13 messages
- Page 1 sur 1
Pour une fonction de ce type là où on ne sait pas vraiment résoudre exactement les équations de la forme f(x)=y avec y fixé, tu va avoir du mal à trouver une méthode autre que l'étude des variations.
En plus les réponses sont
a) ni injective, ni surjective
b) injective mais pas surjective
c) bijective
En plus les réponses sont
a) ni injective, ni surjective
b) injective mais pas surjective
c) bijective
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Bonsoir,
bon, en supposant que tu connais rigoureusement la définition de ce que c'est une injection, une surjection, une bijection (ce qui est le minimum), soit tu utilises la définition formelle de ces notions pour justifier ta réponse, soit tu utilises le tableau de variation.
En loccurrence, si la fonction n'est pas strictement monotone sur l'intervalle considéré, alors elle ne saurait être injective, et a fortiori bijective. De même pour la surjectivité, les flèches dans ton tableau sont censées "parcourir" tout l'ensemble d'arrivée (d'où l'importance de trouver et d'indiquer sur le tableau la valeur des extremum).
Pour I=J=R par exemple, on voit bien à l'aide du tableau que la fonction décroît avant de croître donc c'est mort pour l'injection car dans le sous-intervalle [-4;0], par exemple, la fonction prend plusieurs fois la même valeur.
Pour la surjectivité, bah on voit bien qu'il n'existe pas de x dans R tel que f(x)=y avec y inférieur ou égale à -0.5 puisque la fonction atteint son minimum pour x=-1 et que ce minimum vaut approximativement -0.368.
bon, en supposant que tu connais rigoureusement la définition de ce que c'est une injection, une surjection, une bijection (ce qui est le minimum), soit tu utilises la définition formelle de ces notions pour justifier ta réponse, soit tu utilises le tableau de variation.
En loccurrence, si la fonction n'est pas strictement monotone sur l'intervalle considéré, alors elle ne saurait être injective, et a fortiori bijective. De même pour la surjectivité, les flèches dans ton tableau sont censées "parcourir" tout l'ensemble d'arrivée (d'où l'importance de trouver et d'indiquer sur le tableau la valeur des extremum).
Pour I=J=R par exemple, on voit bien à l'aide du tableau que la fonction décroît avant de croître donc c'est mort pour l'injection car dans le sous-intervalle [-4;0], par exemple, la fonction prend plusieurs fois la même valeur.
Pour la surjectivité, bah on voit bien qu'il n'existe pas de x dans R tel que f(x)=y avec y inférieur ou égale à -0.5 puisque la fonction atteint son minimum pour x=-1 et que ce minimum vaut approximativement -0.368.
Y'a une petite faute de frappe là :
A mon avis, le truc pour mémoriser tout les cas, c'est ça :
a) La fonction
- N'est pas injective car les deux éléments distincts 2 et -2 de l'ensemble de départ ont la même image=f_1(-2)) alors que
alors que 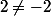
- N'est pas surjective car l'élément -5 de l'ensemble d'arrivé n'a pas d'antécédents : il n'y a pas de réel x tel que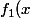=-1) .
.
b) La fonction
- N'est pas injective (preuve identique au a))
- Est surjective car tout y de l'ensemble d'arrivé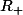 a au moins un antécédent (plus précisément 0 a un seul antécédent 0 et les
a au moins un antécédent (plus précisément 0 a un seul antécédent 0 et les 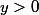 ont 2 antécédents qui sont
ont 2 antécédents qui sont 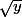 et
et  )
)
c) La fonction
- Est injective car, lorsque deux réels positifs ont le même carré, c'est forcément qu'il sont égaux.
- N'est pas surjective (preuve identique au a))
d) La fonction
- Est injective (preuve identique au c)
- Est surjective (preuve identique au b))
Elle est donc bijective et sa bijection réciproque est
Est ce que tu arrive maintenant à voir pourquoi ta fonction b) n'est pas surjective ?
Donc la surjectivité de la fonction (contrairement à l'injectivité), il faut regarder ce qu'on t'a donné comme ensemble d'arrivé pour la fonction et vérifier que tout les éléments de l'ensemble d'arrivé on bien au moins un antécédent, c'est à dire que, pour tout y de l'ensemble d'arrivé qu'on t'a donné, il y a au moins un x tel que f(x)=y.Archibald a écrit:De même pour la surjectivité, les flèches dans ton tableau sont censées "parcourir" tout l'ensemble d'arrivé (d'où l'importance de trouver et d'indiquer sur le tableau la valeur des extremum).
A mon avis, le truc pour mémoriser tout les cas, c'est ça :
a) La fonction
- N'est pas injective car les deux éléments distincts 2 et -2 de l'ensemble de départ ont la même image
- N'est pas surjective car l'élément -5 de l'ensemble d'arrivé n'a pas d'antécédents : il n'y a pas de réel x tel que
b) La fonction
- N'est pas injective (preuve identique au a))
- Est surjective car tout y de l'ensemble d'arrivé
c) La fonction
- Est injective car, lorsque deux réels positifs ont le même carré, c'est forcément qu'il sont égaux.
- N'est pas surjective (preuve identique au a))
d) La fonction
- Est injective (preuve identique au c)
- Est surjective (preuve identique au b))
Elle est donc bijective et sa bijection réciproque est
Est ce que tu arrive maintenant à voir pourquoi ta fonction b) n'est pas surjective ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
d'accord ! je ne faisais pas la distinction entre ensemble d'arrivée et de départ en fait.
Vous avez pris un exemple ici car ma fonction est xe^x ?
Si j'applique votre raisonnement :
a) La fonction de R-->R de xe^x: n'est pas injective car deux x distincts de l'ensemble de départ ont la même image. N'est pas injective car l'élément ???
b) I=J=[1;+oo[ injective car strictement croissante et non surjective car
c) I=J=[0;+oo[: injective car strictement croissante et deux x identiques ont même image
Malgré votre explication, je ne parviens pas à justifier pour surjective. Je n'arrive pas à bien visualiser :(
Vous avez pris un exemple ici car ma fonction est xe^x ?
Si j'applique votre raisonnement :
a) La fonction de R-->R de xe^x: n'est pas injective car deux x distincts de l'ensemble de départ ont la même image. N'est pas injective car l'élément ???
b) I=J=[1;+oo[ injective car strictement croissante et non surjective car
c) I=J=[0;+oo[: injective car strictement croissante et deux x identiques ont même image
Malgré votre explication, je ne parviens pas à justifier pour surjective. Je n'arrive pas à bien visualiser :(
a) La fonction de R-->R de xe^x: n'est pas injective car deux x distincts de l'ensemble de départ ont la même image : oui, ça se voit sur le tableau de variation. Elle descend jusqu'à un certain yo=f(xo) puis elle remonte donc si on prend un y un peu plus grand que yo, il va y avoir DEUX x DIFFERENTS tels que f(x)=y (un avant xo, l'autre après xo)
N'est pas surjective car si on prend un y strictement plus petit que le yo il n'y a pas de x tels que f(x)=y (y n'a pas d'antécédents).
b) I=J=[1;+oo[ injective car strictement croissante et non surjective car f(1)=(...calcul)>1 donc si on prend un y strictement compris entre 1 et f(1) (donc appartenant à l'ensemble d'arrivé), il n'aura pas d'antécédents
c) I=J=[0;+oo[: injective car strictement croissante <- ça c'est O.K. : vu qu'elle est strictement croissante, si on prend deux éléments distinct x1 et x2 de l'ensemble de départ, il y aura un des deux qui sera < que l'autre donc l'image de ce "plus petit" sera < l'image de l'autre et on ne pourra pas avoir f(x1)=f(x2)
et deux x identiques ont même image <- ça c'est stupide : si tu prend une fonction absolument quelconque, deux x identiques auront forcément la même image (c'est quasiment la définition d'une "fonction") pour montrer qu'une fonction est injective, c'est la réciproque de ça qu'il faut montrer : si deux éléments ont même image alors ils sont égaux. Et comme trés souvent, entre une proposition et sa réciproque, ça n'a rien à voir l'un avec l'autre...
Elle est surjective car f(0)=0, f(x) tend vers +oo lorsque x tend vers +oo, f est continue donc le théorème des valeurs intermédiaires nous assure que tout y entre 0 et +oo admet au moins un antécédent.
N'est pas surjective car si on prend un y strictement plus petit que le yo il n'y a pas de x tels que f(x)=y (y n'a pas d'antécédents).
b) I=J=[1;+oo[ injective car strictement croissante et non surjective car f(1)=(...calcul)>1 donc si on prend un y strictement compris entre 1 et f(1) (donc appartenant à l'ensemble d'arrivé), il n'aura pas d'antécédents
c) I=J=[0;+oo[: injective car strictement croissante <- ça c'est O.K. : vu qu'elle est strictement croissante, si on prend deux éléments distinct x1 et x2 de l'ensemble de départ, il y aura un des deux qui sera < que l'autre donc l'image de ce "plus petit" sera < l'image de l'autre et on ne pourra pas avoir f(x1)=f(x2)
et deux x identiques ont même image <- ça c'est stupide : si tu prend une fonction absolument quelconque, deux x identiques auront forcément la même image (c'est quasiment la définition d'une "fonction") pour montrer qu'une fonction est injective, c'est la réciproque de ça qu'il faut montrer : si deux éléments ont même image alors ils sont égaux. Et comme trés souvent, entre une proposition et sa réciproque, ça n'a rien à voir l'un avec l'autre...
Elle est surjective car f(0)=0, f(x) tend vers +oo lorsque x tend vers +oo, f est continue donc le théorème des valeurs intermédiaires nous assure que tout y entre 0 et +oo admet au moins un antécédent.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:et deux x identiques ont même image <- ça c'est stupide : si tu prend une fonction absolument quelconque, deux x identiques auront forcément la même image (c'est quasiment la définition d'une "fonction") pour montrer qu'une fonction est injective, c'est la [COLOR=Green]réciproque de ça qu'il faut montrer : si deux éléments ont même image alors ils sont égaux. Et comme trés souvent, entre une proposition et sa réciproque, ça n'a rien à voir l'un avec l'autre...[/COLOR]
[/COLOR]
sa contraposée, plutôt.
... non nonArchibald a écrit:sa contraposée, plutôt.
Elle a écrit "deux x identiques ont même image" (
La contraposé de ce qu'elle a écrit c'est "si deux éléments n'ont pas la même image alors ils ne sont pas identiques" (
A la limite, si la réciproque de ce qu'elle a écrit, c'est à dire "si deux éléments ont même image ils sont identiques" (
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
