Dm de maths sur les limites et fonctions continues (urgent)
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
kelly65
- Membre Naturel
- Messages: 71
- Enregistré le: 28 Oct 2013, 05:21
-
 par kelly65 » 23 Nov 2013, 09:12
par kelly65 » 23 Nov 2013, 09:12
Pour tout entier

on considère la fonction la fonction
)
définie sur [0; +

] par :
 = \frac{1}{1+x^n})
On note
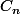
la courbe représentative de la fonction
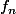
1) a. Déterminer, pour

, les variations de
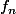
b. Démontrer que les courbes
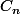
passent toutes par deux points fixes que l'on déterminera
c. Soient deux entiers n et m non nuls avec

.
Comparer
)
et
)
selon les valeurs de x.
En déduire les positions relatives de
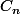
et

.
Après le reste c'est par rapport à des courbes et je ne peux pas mettre l'image
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 23 Nov 2013, 09:19
par Carpate » 23 Nov 2013, 09:19
kelly65 a écrit:Pour tout entier

on considère la fonction la fonction
)
définie sur [0; +

] par :
 = \frac{1}{1+x^n})
On note
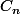
la courbe représentative de la fonction
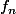
1) a. Déterminer, pour

, les variations de
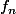
b. Démontrer que les courbes
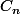
passent toutes par deux points fixes que l'on déterminera
c. Soient deux entiers n et m non nuls avec

.
Comparer
)
et
)
selon les valeurs de x.
En déduire les positions relatives de
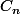
et

.
Après le reste c'est par rapport à des courbes et je ne peux pas mettre l'image
Bonjour Kelly65,
Tu ne dis pas bonjour, tu marques un "urgent"dans ton titre et tu n'indiques pas ce que tu as fait et ce qui te pose problème !
Ca fait beaucoup et n'incite pas à te répondre.
Qu'attends-tu de nous ? Qu'on te fournisse une solution toute prête à recopier ?
-
kelly65
- Membre Naturel
- Messages: 71
- Enregistré le: 28 Oct 2013, 05:21
-
 par kelly65 » 23 Nov 2013, 11:22
par kelly65 » 23 Nov 2013, 11:22
Carpate a écrit:Bonjour Kelly65,
Tu ne dis pas bonjour, tu marques un "urgent"dans ton titre et tu n'indiques pas ce que tu as fait et ce qui te pose problème !
Ca fait beaucoup et n'incite pas à te répondre.
Qu'attends-tu de nous ? Qu'on te fournisse une solution toute prête à recopier ?
Bonjour,
Je n'attends pas une solution toute faite.
Pour le a) il faut que je calcule la dérivée c'est ça ? Ou je dois chercher les limites de la fonction ?
J'ai essayé de faire la dérivée et ça me donne fn'(x) = (0*(1+x^2))+(1*(nx^(n-1))/((1+x^n)^2) = nx^(n-1) / ((1+x^n)^2)
Et (1+x^n)^2 > 0 donc la dérivée est du signe de nx^(n-1) et ce terme est toujours positif donc la dérivée est positive pour n supérieur ou égal à 1 donc la fonction fn est croissante, c'est ça ?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 23 Nov 2013, 11:47
par Carpate » 23 Nov 2013, 11:47
kelly65 a écrit:Bonjour,
Je n'attends pas une solution toute faite.
Pour le a) il faut que je calcule la dérivée c'est ça ? Ou je dois chercher les limites de la fonction ?
J'ai essayé de faire la dérivée et ça me donne fn'(x) = (0*(1+x^2))+(1*(nx^(n-1))/((1+x^n)^2) = nx^(n-1) / ((1+x^n)^2)
Et (1+x^n)^2 > 0 donc la dérivée est du signe de nx^(n-1) et ce terme est toujours positif donc la dérivée est positive pour n supérieur ou égal à 1 donc la fonction fn est croissante, c'est ça ?
Il est recommandé de commencer par fixer le domaine de définition de f. Quel est-il ?
Erreur de signe :
=\frac{-nx^{n-1}}{(1+x^n)^2})
a) n pair , donc n-1 pair :
)
décroissante sur R
b) n impair, n-1 impair : distinguer les cas x negatif et x positif
EDIT J'avais mal l'énoncé et n'avais pas vu que le domaine de variation était limité par l'énoncé à

Donc
)
décroissante sur ce domaine
-
kelly65
- Membre Naturel
- Messages: 71
- Enregistré le: 28 Oct 2013, 05:21
-
 par kelly65 » 23 Nov 2013, 13:48
par kelly65 » 23 Nov 2013, 13:48
si n est pair, n-1 n'est pas pair non ?
-
kelly65
- Membre Naturel
- Messages: 71
- Enregistré le: 28 Oct 2013, 05:21
-
 par kelly65 » 23 Nov 2013, 14:03
par kelly65 » 23 Nov 2013, 14:03
Carpate a écrit:Il est recommandé de commencer par fixer le domaine de définition de f. Quel est-il ?
Erreur de signe :
=\frac{-nx^{n-1}}{(1+x^n)^2})
a) n pair , donc n-1 pair :
)
décroissante sur R
b) n impair, n-1 impair : distinguer les cas x negatif et x positif
EDIT J'avais mal l'énoncé et n'avais pas vu que le domaine de variation était limité par l'énoncé à

Donc
)
décroissante sur ce domaine
Et dans mon cours c'est marqué que la dérivée de 1/x^n c'est - n/x^(n-1). La seule différence ici c'est qu'il y a le 1 en plus au dénominateur et la dérivée de 1 c'est 0 donc on en prends pas compte
-
kelly65
- Membre Naturel
- Messages: 71
- Enregistré le: 28 Oct 2013, 05:21
-
 par kelly65 » 23 Nov 2013, 14:28
par kelly65 » 23 Nov 2013, 14:28
Non oublie mon dernier message, tu as raison
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 23 Nov 2013, 15:48
par Carpate » 23 Nov 2013, 15:48
kelly65 a écrit:Non oublie mon dernier message, tu as raison
As-tu trouvé les 2 points fixes ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 107 invités
on considère la fonction la fonction
définie sur [0; +
] par :
la courbe représentative de la fonction
, les variations de
passent toutes par deux points fixes que l'on déterminera
.
et
selon les valeurs de x.
et
.
décroissante sur R
décroissante sur ce domaine