Application linéaire

[baigori]

Merci bien, et merci à nightmare

[Youss]

Bonjour, j'ai un exercice en algèbre linéaire mais je n'arrive pas à le faire.

Voici l'exo :

Montrer que les applications suivantes sont des automorphismes de R² :

f(x,y)=(x+y,x)

Je sais qu'il y a 2 étapes pour montrer que c'est un automorphisme :

1ère : montrer qu'elle est linéaire (j'ai réussi)
2ème: qu'elle est bijective, c'est ici ou je bloque. Je sais que pour qu'elle soit bijective, il faut que la base de E soit une base de F et que le rang(f)=dimE=dimF. Le probléme c'est que dans l'énoncé, il nous dise pas si c'est E-->F ou seulement E-->E ?

Si vous pouvez m'aider, ca serait cool.

[Archibald]

Bonsoir,

soit une application de E vers F. est un automorphisme ssi :
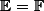(1) + bijective (2)

(1) traduit que est un endomorphisme
(2) traduit que est un isomorphisme

Dans ton cas, f est une application qui à chaque couple lui associe son image (encore un couple dans )

Nous avons donc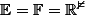 et la première condition est remplie.

Quant à la seconde, tu sais que f bijective = f injective + f surjective.
Or comme nous sommes en dimension finie et que nous avons précédemment vérifié que f est un endomorphisme,
nous avons cette équivalence : f bijective f injective f surjective

Concrètement, nous avons seulement besoin de montrer que f est injective ou f surjective.

Montre par ex que f est injective, soit que son noyau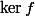 est réduit au vecteur nul