Je vais décrire l'esprit dans lequel j'ai codé l'algorithme pour créer le tournoi.
Pour
N équipes, il y a exactement N/2*(N-1) connections distinctes, où la connection signifie 'se voir dans une poule'. On peut organiser ces connections dans la partie triangulaire supérieure d'une matrice d'adjacence NxN, que j'apppelle
C. Similairement à l'idée de fatal_error,
C contient le nombre de fois que les couples se voient tout au long du tournoi.
R est la matrice des rencontres. Chaque ligne correspond à un nouveau jour.
Exemple: 9 équipes, 3 poules de 3, 6 Rencontres.
 Optimisation
Optimisation:
Je souhaite que toutes les équipes se voient et je veux éviter le plus possible les répétitions. Dans ce sens, l'exemple du dessus n'est pas bon. Par exemple, les équipes 5 et 9 se voient 4 fois, alors que les équipes 4 et 8 ne rencontrent jamais l'équipe 9.
Je crée une mesure d'optimalité
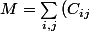^2)
. La somme des entrées de
C est constante pour un tournoi donné, puisque les poules ne varient pas, créant ainsi toujours le meme nombre de 'vus' par journées. Ainsi, en élevant les entrées au carré, et en minimisant M, je m'assure d'enlever les grands nombres (beaucoup de rencontres identiques), et puisque la somme des entrées est constante, je m'assure par la même occasion d'enlever beaucoup de 0s dans
C.
Exemple optimisé 
Au sens de ma mesure, il s'agit là de l'optimum absolu. Je ne peux pas éviter plus de 2 que ci-dessus.
Calculer M Optimum L'algorithme reçoit un M_Optimum, et génère intelligemment des tournois. Il y a une composante aléatoire, et donc il réessaye jusqu'à atteindre M_Optimum.
Le calcul de M_Opt :
Nombre de connections distinctes :
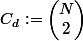
. Nombre connections créées lors d'un tournoi de J jours et poule
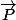
:

.
Ainsi, dans le cas optimal, le nombre de fois que les équipes se voient varie entre
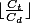
et
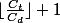
. Dans le cadre de l'exemple,
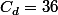
et
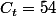
. Il faut donc distribuer 54 'vus' sur 36 emplacements, ce qui signifie que le nombre de vus variera entre 1 et 2.
En toute generalite, si l'on appelle
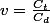
alors la matrice d'adjacence optimale contient
\right))
entrées valant
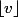
et
)
entrées valant
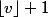
. Sur l'exemple, cela se vérifie aisément : v = 3/2, Nombre de 1 : 36*1/2 = 18, Nombre de 2 : 36*1/2 = 18. Donc, l'optimum vaut 18*1^2+18*2^2 = 90.
Faute du calcul de M_Optimum Si l'on prend l'exemple N=11, Poules = [4 4 3], J = 2, l'algorithme n'aboutira jamais.
En effet, on a
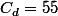
,
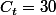
. Toutes les entrées varient donc entre 0 et 1. La matrice optimale doit contenir 30 fois 1, et 25 fois 0. Donc l'algorithme essaye de chercher ce tableau. Sauf qu'à cause de la structure de poules, dès le 2ème jour, il y a forcément 2 fois un "2" qui traîne quelque part dans la matrice d'adjacence. Donc le M_Optimum véridique est plus élevé que celui que cherche l'algorithme.
Conclusions Dans certains cas, l'algorithme converge très vite à la solution optimale (moins de 10 secondes pour le premier tableau 9 optimisé), dans d'autres il converge lentement (1 heure pour 15 à 5 poules de 3). J'aimerais donc éviter d'attendre X heures pour être sûr que l'algorithme ne peut pas faire mieux. Je voudrais avoir un moyen de recalculer M_Optimum pour les cas pathologiques.
C'est afin d'avoir une méthode pour recalculer M_Optimum que je me tourne vers vous.
PS:
Fatal_error, j'ai cherché des symétries, mais dès que tu commences à avoir des poules mixtes de 4 et 3, la structure qu'engendre la poule de 4 dans la matrice d'adjacence n'a pas de symétrie particulière. Ca te fait des hexagones plus ou moins éfilés..De plus, mon algorithme fonctionne très bien pour trouver les tableaux. Ce que tu fais c'est enfait simuler un tournoi, et tu conclus à partir de la simulation. Moi, j'aimerais une caractérisation rapide de ces cas pathologiques pour recalculer mon optimum, et être sûr que mon algorithme a convergé.
