Exercice généralisé sur les coniques

[ThekamikazeFou]

Bonjour, voilà je ne comprends pas grand chose à ce chapitre....

en réalité ce que je n'arrive pas à faire, c'est trouver les sommets et les nouveaux axes avec les asymptotes.

prenons un exemple : soit : 5x^2+8xy+5y^2-18ax-18ay+9a^2=0

je sais qu'il s'agit d'une ellipse.
que le centre est C(a,a)

ici les pentes sont -1 et 1 puisque f(x,y)=f(y,x)
or si cette égalité n'était pas vérifier, comment retrouver les pentes du nouvel axe?

maintenant recherchons les sommets de l'ellipse dans le repère d'origine.
j'ai deux possibilité :
soit je fais je résous f(x,y)=0 en posant y=x (ou y=-x)
soit j'utilise un système de ce type :
f(x,y)=0
x=a+t
y=a-t


ma question est simple, pourquoi?


les réponses peuvent être longue a expliquer mais je ne comprends rien, alors merci d'être assez précis.

[chan79]

Salut
tu as des infos ici

[ThekamikazeFou]

merci, sauf que je ne souhaite pas recommencer tout le cours que j'ai eu, j'ai n'ai jamais utilisé les matrices dans les coniques, du moins très rarement.
de plus la méthode proposé me semble bien compliquée...

[chan79]

merci, sauf que je ne souhaite pas recommencer tout le cours que j'ai eu, j'ai n'ai jamais utilisé les matrices dans les coniques, du moins très rarement.
de plus la méthode proposé me semble bien compliquée...

Salut
Tu peux essayer de suivre la démarche sur un exemple.

[Skullkid]

merci, sauf que je ne souhaite pas recommencer tout le cours que j'ai eu, j'ai n'ai jamais utilisé les matrices dans les coniques, du moins très rarement.
de plus la méthode proposé me semble bien compliquée...

Malheureusement, pour réduire une conique, il faut faire des calculs. Le lien de chan79 donne la méthode générale. On peut la présenter un peu différemment mais ça ne la rendra pas plus simple. Dans le cas que tu donnes on peut court-circuiter parce que ton équation a des symétries évidentes, mais si je te donne une équation moins sympathique, genre 25x^2+66y^2+20xy-5x-12y-20 = 0, il faut utiliser la méthode donnée dans le lien de chan79 pour s'en sortir.

Soit tu es censé savoir réduire toutes les coniques, auquel cas il va falloir apprendre la méthode, de préférence de la faon dont elle est présentée dans ton cours, soit tu es juste censé être capable de repérer des symétries pas trop cachées et on ne te présentera que des cas "simples".

Pour ce qui est de ta deuxième question, tu connais le centre et les axes (d'ailleurs, comment as-tu trouvé le centre ?). Les sommets sont les intersections entre l'ellipse et un de ses axes, donc tu résous le système qui correspond à "(x,y) appartient à l'ellipse et (x,y) appartient à tel axe". Appartenir à l'ellipse ça se traduit par f(x,y) = 0, appartenir à un axe ça se traduit par une équation de droite, soit sous forme cartésienne (x = y pour l'axe de pente 1, x + y = 2a pour l'axe de pente -1) soit sous forme paramétrique ({x = a+t et y = a+t} pour l'axe de pente 1, {x = a+t et y = a-t} pour l'axe de pente -1).

[Ben314]

Je rajouterais bien que vouloir faire des changement de repères (orthogonaux du plan) quand on ne connait pas bien les matrices 2x2, ça va pas être super facile de trouver comment faire, ni de comprendre le "pourquoi" on fait comme ça...

[ThekamikazeFou]

merci pour vos réponses !
alors tout d'abord je pense que je n'ai eut que des axe de symétrie évident visiblement puisque je n'ai pas utilisé de matrice ( ou peut être, mais je n'en n'ai jamais vu écrite pour ce cours.)
pour la paramétrisation que j'ai donné, je l'avais plus ou moins comprise. Mais si par exemple lest axes sont de ce type :

2x-1 et 3x+y comment paramétrer?

Ben314, je métrise bien les matrice 2x2, d'ailleurs toute les matrices, mais le problème c'est que je souhaite comprendre la méthode que le prof nous à donné. Or il saute tellement d'étape dans les calculs qu'on ne comprend pas tout malheureusement...

[Ben314]

Peut-être que les autres ont d'autre façon (plus simples...) de voir les choses, personnellement, je vois vraiment ça comme un problème de changement de repère.
Le truc à savoir (et c'est plus facile à comprendre avec les matrices), c'est que si on a deux repère orthonormés directs tout les deux et qu'un même point M a pour coordonnées (x,y) dans le premier et (X,Y) dans le second alors on a :


où sont les coordonnées (dans le premier repère) du centre O' du deuxième repère (qui a évidement comme coordonnées (X=0,Y=0) dans le second repère !)
Et est l'angle (orienté) entre la demi droite [Ox[ du premier repère et la demi droite [O'X[ du second repère.
Quand tu as l'équation d'une conique en x et y, tu remplace les x et les y par les expressions correspondantes çi dessus et tu cherche les valeurs de , , pour que la nouvelle équation en X et Y soit de la forme .

En fait, pour et ce n'est pas compliqué (c'est à peu prés la même chose que la mise sous forme canonique d'une équation du 2nd degré).
Mais pour , c'est un peu plus compliqué : c'est lui qui doit faire "disparaitre" les termes en 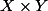que l'on a dans l'équation.

[Skullkid]

Je sais pas ce qu'est un "axe de type 2x+1". Si une droite est donnée par une équation cartésienne, tu peux en donner un point A(a1,a2) et un vecteur directeur u(u1,u2). Une paramétrisation de ta droite est le système {x = a1 + t*u1 et y = a2 + t*u2}.

[ThekamikazeFou]

Ok super, merci a vous, je pense que ça devrait m'aider à mieux comprendre tout ça !

en réalité c'est le changement de repère et d'axe qui me perturbe, puisqu'il n'existe aucune formule dans ces cas là !

merci.