Suites, exercices TS
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Nonolie
- Membre Naturel
- Messages: 11
- Enregistré le: 05 Sep 2006, 17:26
-
 par Nonolie » 06 Sep 2006, 13:36
par Nonolie » 06 Sep 2006, 13:36
Voila quelques petits exercices que je n'arrive pas à résoudre... :cry: Si vous pouvez m'aider au moins sur l'un deux... pliiiizzzzzz :ptdr:
Exercice 1 :
On pose :
S indice n = 1 + 2/3 + (2/3)^2 + ... + (2/3)^n
A l'aide d'une formule sommatoire, montrer que S indice n est inférieur ou égal a 3.
Exercice 2 :
Déterminer la limite éventuelle des suites de termes généraux :
U indice n = n^2 + racine de n
V indice n = n(3-n)
W indice n = 1/(n^2-5)
exercice 3 :
Etudier la limite de la suite S indice n :
S indice n = 1 + x + x^2 + ... + x^n (avec -1 < x <1 )
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 06 Sep 2006, 13:47
par nekros » 06 Sep 2006, 13:47
Salut,
Pour l'exo 1 et 2, reconnais des suites géométriques.
Je te montre pour le 1 :
On a
=\sum_{k=0}^n (\frac{2}{3})^k = \frac{1-(\frac{2}{3})^{n+1}}{1-(\frac{2}{3})}=3 (1-(\frac{2}{3})^{n+1}))
Or,
^{n+1} \le 1)
donc ...
Continue.
A+
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 06 Sep 2006, 13:50
par Flodelarab » 06 Sep 2006, 13:50
ou bloques tu ?
-
Nonolie
- Membre Naturel
- Messages: 11
- Enregistré le: 05 Sep 2006, 17:26
-
 par Nonolie » 06 Sep 2006, 13:54
par Nonolie » 06 Sep 2006, 13:54
Un peu partout... Pour le premier exercice, j'ai utilisé la formule sommatoire qui correspond, et je tombe sur 3... Comme si, pour tt n, c'était toujours égal a trois...
Et puis pour les deux autres, ben je bloque de partout...
Un peu d'aide supplémentaire pliiizz :ptdr:
Merci a vous, c'est deja très gentil de m'aider un peu...
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 06 Sep 2006, 13:55
par nekros » 06 Sep 2006, 13:55
Regarde mon post :lol4:
Et essaie de faire les autres.
A+
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 06 Sep 2006, 13:59
par nekros » 06 Sep 2006, 13:59
Tu comprends ?
-
Nonolie
- Membre Naturel
- Messages: 11
- Enregistré le: 05 Sep 2006, 17:26
-
 par Nonolie » 06 Sep 2006, 14:01
par Nonolie » 06 Sep 2006, 14:01
Raaahhh... mais comment sais tu que c'est inférieur ou égal a 1???
ah c'est bon, je viens de comprendre... merciiiiii !!!!
Si cela est inférieur a 1, alors le reste est inférieur a 3... héhéhééé !! Vive les math, les mateux... et toi en particulier !! merciii !!
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 06 Sep 2006, 14:03
par nekros » 06 Sep 2006, 14:03
Nonolie a écrit:Raaahhh... mais comment sais tu que c'est inférieur ou égal a 1???
ah c'est bon, je viens de comprendre... merciiiiii !!!!
Tu retranches une quantité positive à 1 !
Ou si tu veux le tout tend vers 1, donc il est inférieur ou égale à 1.
A+
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 06 Sep 2006, 14:05
par nekros » 06 Sep 2006, 14:05
Ok de rien.
Essaie de faire l'exo 3, c'est le même genre.
Au fait, tu connais la somme s'une suite géométrique ?
-
Nonolie
- Membre Naturel
- Messages: 11
- Enregistré le: 05 Sep 2006, 17:26
-
 par Nonolie » 06 Sep 2006, 14:06
par Nonolie » 06 Sep 2006, 14:06
Et pour calculer S indice 50, je mets 2/3 a la puissance 51, c'est ca??
La somme d'une suite géomatrique, nan je ne vois pas...
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 06 Sep 2006, 14:10
par BancH » 06 Sep 2006, 14:10
Nonolie a écrit:Et pour calculer S indice 50, je mets 2/3 a la puissance 51, c'est ca??
Oui mais tu ne peux pas calculer la valeur exacte, par contre tu vois bien que

-
Nonolie
- Membre Naturel
- Messages: 11
- Enregistré le: 05 Sep 2006, 17:26
-
 par Nonolie » 06 Sep 2006, 14:11
par Nonolie » 06 Sep 2006, 14:11
pour l'exo 3, je tombe sur :
(1 - x^(n+1))/(1-x)... mais alors la... ?????
Sinan, merci pour l'exercice1, j'ai réussit a le faire et figure toi que j'ai meme compris... Ce qui est un exploit !! hihi !! ^^
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 06 Sep 2006, 14:16
par nekros » 06 Sep 2006, 14:16
Nonolie a écrit:La somme d'une suite géomatrique, nan je ne vois pas...
Dans ce cas, tu multiplies par x la somme :
Tu as
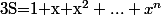
Donc
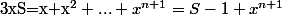
Donc
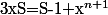
soit
=-1+x^{n+1})
soit

-
Nonolie
- Membre Naturel
- Messages: 11
- Enregistré le: 05 Sep 2006, 17:26
-
 par Nonolie » 06 Sep 2006, 14:18
par Nonolie » 06 Sep 2006, 14:18
Xcuse moi Nekros, mais je ne comprends rien du tt...
Est ce que vous pourriez simplement me mettre sur la voie pour la premiere suite de l'exercice 2 svp??? :ptdr:
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 06 Sep 2006, 14:18
par nekros » 06 Sep 2006, 14:18
Nonolie a écrit:Xcuse moi Nekros, mais je ne comprends rien du tt...
Ce n'est pas grave, tu as trouvé.
Maintenant, il faut étudier la limite : tu n'as aucune idée ?
A+
EDIT : salut Banch :happy3:
-
Nonolie
- Membre Naturel
- Messages: 11
- Enregistré le: 05 Sep 2006, 17:26
-
 par Nonolie » 06 Sep 2006, 14:20
par Nonolie » 06 Sep 2006, 14:20
Exercice 2 :
je dirais que pour Un, la limite est + infini parce que n^2 tend vers +infini et racine de n aussi... Je suis sur la bonne voie??
Exercice 3 :
je dirais que Sn tend vers zéro puisqu'une fois établie avec la formue sommatoire, le dénominateur tend vers zéro et le numérateur aussi... alors?? héhéhé...
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 06 Sep 2006, 14:21
par nekros » 06 Sep 2006, 14:21
Nonolie a écrit:Xcuse moi Nekros, mais je ne comprends rien du tt...
Est ce que vous pourriez simplement me mettre sur la voie pour la premiere suite de l'exercice 2 svp??? :ptdr:
Essaie de terminer le 3 !
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 06 Sep 2006, 14:22
par BancH » 06 Sep 2006, 14:22
nekros a écrit:salut Banch :happy3:
Salut à toi !
Au fait, il vient d'où ton nom ? Ca me fait toujours penser à nécromancien.
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 06 Sep 2006, 14:24
par nekros » 06 Sep 2006, 14:24
BancH a écrit:Salut à toi !
Au fait, il vient d'où ton nom ? Ca me fait toujours penser à nécromancien.
:ptdr:
C'est un personnage dans Warcraft
-
Nonolie
- Membre Naturel
- Messages: 11
- Enregistré le: 05 Sep 2006, 17:26
-
 par Nonolie » 06 Sep 2006, 14:24
par Nonolie » 06 Sep 2006, 14:24
regarde mon post, j'ai émis mes hypotheses de réponses (justes.)..
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités
