Racines emboitées.

par **Sourire_banane** » 02 Nov 2013, 13:26

Bonjour,

Prouver que pour tout x>1 on peut trouver y>0 tel que :

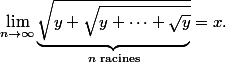
Bonne chance !

par **leon1789** » 02 Nov 2013, 13:35

Sourire_banane a écrit:Bonjour,

Prouver que pour tout x>1 on peut trouver y>0 tel que :

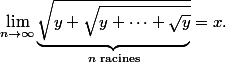
Bonne chance !

Analysons le problème :
si la conclusion est vraie alors

donc

.

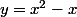
On vient de montrer que seul

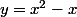
peut convenir. Il n'y a plus qu'à vérifier :
Posons

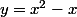
. Alors y > 0 car x > 1, donc

.
Définissons la suite

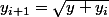
avec y_0 = 0.
Elle est strictement positive, monotone, convergente vers x ?

par **leon1789** » 02 Nov 2013, 13:49

Sourire_banane a écrit:Bonjour,

Prouver que pour tout x>1 on peut trouver y>0 tel que :

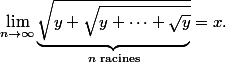
Bonne chance !

Analysons le problème :
si la conclusion est vraie alors

donc

.
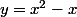
On vient de montrer que seul

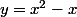
peut convenir. Il n'y a plus qu'à vérifier !

Posons

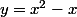
. Alors y > 0 car x > 1, donc

.
Définissons la suite

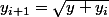
avec

.
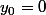
Elle est strictement positive, monotone, convergente vers x ?

par **nodjim** » 02 Nov 2013, 13:58

Ou encore
f²(y)=y+f(y)
équation du second degré qui aboutit à f(y)=(1+rac(1+4y))/2 pour la solution positive.

par **Ben314** » 02 Nov 2013, 15:35

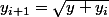
leon1789 a écrit:Définissons la suite avec .
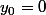
Elle est strictement positive, monotone, convergente vers x ?

La croissance est évidente (pour passer de y_i à y_{i+1} on peut remplacer le dernier y dans la suite de racines emboitées définissant y_i par

ce qui fait augmenter le résultat).
La suite y_i est majorée par x vu que

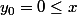
et que, si

alors

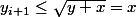
La suite converge donc vers L tel que

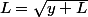
donc L=x.

par **leon1789** » 02 Nov 2013, 16:40

et vi :lol3:

par **WillyCagnes** » 02 Nov 2013, 17:02

nodjim a écrit:Ou encore
f²(y)=y+f(y)
équation du second degré qui aboutit à f(y)=(1+rac(1+4y))/2 pour la solution positive.

bonsoir, j'avais trouvé la même solution et la formule est très jolie avec y=2