Résoudre une équation
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
artichaud
- Membre Naturel
- Messages: 14
- Enregistré le: 29 Oct 2013, 14:15
-
 par artichaud » 01 Nov 2013, 10:10
par artichaud » 01 Nov 2013, 10:10
Bonjour, je suis coincé sur une équation .... Quelqu'un pourrait-il m'aider ... :$
Voici lénoncé :
Résoudre dans R l'équation

(-x² + 2x +1) = x
Pour l'instant voilà ce que j'ai fait, surtout corrigez moi quand il la faut, je ne suis pas sur que mes pistes sont bonnes ... :/

(-x² + 2x +1) = x
-x² + 2x +1 = x²
Delta = 8>0 donc deux racines :
x1 = 1 +

2
x2 = 1 -

2
OU ALORS 
(-x² + 2x +1) = x
-x² + 2x +1 = x²
2x + 1 = 0
x = -1/2
Mais dans les deux cas, je n'y arrive pas ... et je sais qu'on ne peut pas calculer la racine carrée d'un nombre négatif ...
Enfin bref, je suis à la rammasse, aidez moi s'il vout plaît :mur:
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 01 Nov 2013, 10:21
par Carpate » 01 Nov 2013, 10:21
artichaud a écrit:Bonjour, je suis coincé sur une équation .... Quelqu'un pourrait-il m'aider ... :$
Voici lénoncé :
Résoudre dans R l'équation

(-x² + 2x +1) = x
Pour l'instant voilà ce que j'ai fait, surtout corrigez moi quand il la faut, je ne suis pas sur que mes pistes sont bonnes ... :/

(-x² + 2x +1) = x
-x² + 2x +1 = x² A = \pm B
Delta = 8>0 donc deux racines :
x1 = 1 +

2
x2 = 1 -

2
OU ALORS 
(-x² + 2x +1) = x
-x² + 2x +1 = x²
2x + 1 = 0
x = -1/2
Mais dans les deux cas, je n'y arrive pas ... et je sais qu'on ne peut pas calculer la racine carrée d'un nombre négatif ...
Enfin bref, je suis à la rammasse, aidez moi s'il vout plaît :mur:
Pour la partie "OU ALORS" comment peux-tu justifier le passage de -x² + 2x +1 = x²
à 2x+1 = 0 ?
La première version est la bonne.
Tu as le choix entre 2 méthodes :
1) celle que tu utilises c'est-à-dire élever au carré sans précaution mais tu introduis une solution parasite, donc il te faudra contrôler si les racines obtenues conviennent c'est-à-dire si elles sont positives
2) procéder par équivalence :

(-x^2 + 2x +1) = x est équivalent à
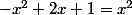
et
x>0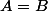
n'est pas équivalent à
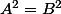
car les solutions de
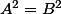
sont
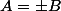
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 01 Nov 2013, 10:36
par Shew » 01 Nov 2013, 10:36
artichaud a écrit:Bonjour, je suis coincé sur une équation .... Quelqu'un pourrait-il m'aider ... :$
Voici lénoncé :
Résoudre dans R l'équation

(-x² + 2x +1) = x
Pour l'instant voilà ce que j'ai fait, surtout corrigez moi quand il la faut, je ne suis pas sur que mes pistes sont bonnes ... :/

(-x² + 2x +1) = x
-x² + 2x +1 = x²
Delta = 8>0 donc deux racines :
x1 = 1 +

2
x2 = 1 -

2
OU ALORS 
(-x² + 2x +1) = x
-x² + 2x +1 = x²
2x + 1 = 0
x = -1/2
Mais dans les deux cas, je n'y arrive pas ... et je sais qu'on ne peut pas calculer la racine carrée d'un nombre négatif ...
Enfin bref, je suis à la rammasse, aidez moi s'il vout plaît :mur:
Le delta est faux il vaut 12 .
-
artichaud
- Membre Naturel
- Messages: 14
- Enregistré le: 29 Oct 2013, 14:15
-
 par artichaud » 01 Nov 2013, 10:45
par artichaud » 01 Nov 2013, 10:45
Carpate a écrit:Pour la partie "OU ALORS" comment peux-tu justifier le passage de -x² + 2x +1 = x²
à 2x+1 = 0 ?
La première version est la bonne.
Tu as le choix entre 2 méthodes :
1) celle que tu utilises c'est-à-dire élever au carré sans précaution mais tu introduis une solution parasite, donc il te faudra contrôler si les racines obtenues conviennent c'est-à-dire si elles sont positives
2) procéder par équivalence :

(-x^2 + 2x +1) = x est équivalent à
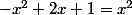
et
x>0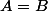
n'est pas équivalent à
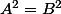
car les solutions de
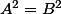
sont
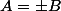
Ah oui mince, pour le "OU ALORS" j'ai fais un grosse bêtise, ce ne serait pas plutôt :

(-x² + 2x +1) = x
-x² + 2x +1 = x²
-2x² + 2x +1 = 0
Enfin si cette solution n'est pas la bonne autant la laisser tomber !

Ici, seulement x1 est positive ...
Mais tes deux propositions se rejoignent, non ?
J'ai bien assimilé ce que tu as dit, mais j'ai l'impression que c'est ce sur quoi j'étais partis au début (ma première proposition) .. :$
Excuse moi, j'ai du mal ... :/
-
artichaud
- Membre Naturel
- Messages: 14
- Enregistré le: 29 Oct 2013, 14:15
-
 par artichaud » 01 Nov 2013, 10:46
par artichaud » 01 Nov 2013, 10:46
Shew a écrit:Le delta est faux il vaut 12 .
Oui je viens de m'apercevoir, merci =)
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 01 Nov 2013, 10:53
par Carpate » 01 Nov 2013, 10:53
artichaud a écrit:Ah oui mince, pour le "OU ALORS" j'ai fais un grosse bêtise, ce ne serait pas plutôt :

(-x² + 2x +1) = x
-x² + 2x +1 = x²
-2x² + 2x +1 = 0
Enfin si cette solution n'est pas la bonne autant la laisser tomber !

Ici, seulement x1 est positive ...
Mais tes deux propositions se rejoignent, non ?
J'ai bien assimilé ce que tu as dit, mais j'ai l'impression que c'est ce sur quoi j'étais partis au début (ma première proposition) .. :$
Excuse moi, j'ai du mal ... :/
Ce que je ne comprends pas c'est pourquoi ce "ou alors" (en plus que la suite comporte une erreur de calcul)
je ne vois aucun rejet de la racine négative dans ce que tu as écrit
-
artichaud
- Membre Naturel
- Messages: 14
- Enregistré le: 29 Oct 2013, 14:15
-
 par artichaud » 01 Nov 2013, 11:38
par artichaud » 01 Nov 2013, 11:38
Ouais bon, on laisse le "OU ALORS" de coté ! ;)
Les deux racines que j'ai trouvé sont bonnes alors ?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 01 Nov 2013, 11:49
par Shew » 01 Nov 2013, 11:49
artichaud a écrit:Ouais bon, on laisse le "OU ALORS" de coté !

Les deux racines que j'ai trouvé sont bonnes alors ?
Non puisque le delta est faux dans votre post principal , il faut donc recalculer les racines en fonction du bon Delta .
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 01 Nov 2013, 11:50
par Carpate » 01 Nov 2013, 11:50
artichaud a écrit:Ouais bon, on laisse le "OU ALORS" de coté !

Les deux racines que j'ai trouvé sont bonnes alors ?
Si tu poses cette question c'est que tu n'as pas lu ce que je t'ai déjà écrit :
T
u as le choix entre 2 méthodes :
1) celle que tu utilises c'est-à-dire élever au carré sans précaution mais tu introduis une solution parasite, donc il te faudra contrôler si les racines obtenues conviennent c'est-à-dire si elles sont positives
2) procéder par équivalence :
 (-x^2 + 2x +1) = x est équivalent à -x^2 + 2x +1 = x^2 et x>0
(-x^2 + 2x +1) = x est équivalent à -x^2 + 2x +1 = x^2 et x>0
-
hbachh
- Membre Naturel
- Messages: 12
- Enregistré le: 01 Nov 2013, 11:22
-
 par hbachh » 01 Nov 2013, 11:52
par hbachh » 01 Nov 2013, 11:52
Salut,
d'apres mes calculs:
-x^2+2x+1=x^2
-2x^2+2x+1=0
Delta=12
x1=-1/2+rac(12)/4
x2=-1/2-rac(12)/4
donc
vu que -x^2+2x+1=x^2 -x^2+2x+1>0
--> rac(-x^2+2x+1)>0 donc x>0
alors, S= -1/2+2*rac(3)
Ps: 2*rac(3)=rac(12)/4
je crois :we:
-
artichaud
- Membre Naturel
- Messages: 14
- Enregistré le: 29 Oct 2013, 14:15
-
 par artichaud » 01 Nov 2013, 12:03
par artichaud » 01 Nov 2013, 12:03
Shew a écrit:Non puisque le delta est faux dans votre post principal , il faut donc recalculer les racines en fonction du bon Delta .
Ah oui, j'avais pas recalculé après avec delta vaut 12 ...
Donc maintenant, je trouve :
x1 = (1+

3)/2
x2 = (1-

3)/2
C'est ça ?
-
hbachh
- Membre Naturel
- Messages: 12
- Enregistré le: 01 Nov 2013, 11:22
-
 par hbachh » 01 Nov 2013, 12:12
par hbachh » 01 Nov 2013, 12:12
je crois que oui et ne lit meme pas le message d'avant, j'ai fait une faute sur la derniere solution :marteau:
-
artichaud
- Membre Naturel
- Messages: 14
- Enregistré le: 29 Oct 2013, 14:15
-
 par artichaud » 01 Nov 2013, 12:18
par artichaud » 01 Nov 2013, 12:18
Carpate a écrit:Si tu poses cette question c'est que tu n'as pas lu ce que je t'ai déjà écrit :
T
u as le choix entre 2 méthodes :
1) celle que tu utilises c'est-à-dire élever au carré sans précaution mais tu introduis une solution parasite, donc il te faudra contrôler si les racines obtenues conviennent c'est-à-dire si elles sont positives
2) procéder par équivalence :
 (-x^2 + 2x +1) = x est équivalent à -x^2 + 2x +1 = x^2 et x>0
(-x^2 + 2x +1) = x est équivalent à -x^2 + 2x +1 = x^2 et x>0
Si j'ai lu, mais j'ai l'impression que c'est ce que j'ai fait, mais je me trompe sans doute alors dans ce cas tu peux me décoincer ?
J'arrive à dire que

(-x² + 2x +1) = x
-x² + 2x +1 = x²
(Dis moi si je me trompe) , -x² + 2x +1 à deux solutions :
* -;)x
*

x
Car -x² + 2x +1 =
x²Peut-être que c'est faux mais j'ai écrit ça sur mon brouillon alors ...
-
artichaud
- Membre Naturel
- Messages: 14
- Enregistré le: 29 Oct 2013, 14:15
-
 par artichaud » 01 Nov 2013, 12:19
par artichaud » 01 Nov 2013, 12:19
hbachh a écrit:je crois que oui et ne lit meme pas le message d'avant, j'ai fait une faute sur la derniere solution :marteau:
D'accord, pas de problème ! Merci quand même

-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 01 Nov 2013, 13:05
par Carpate » 01 Nov 2013, 13:05
artichaud a écrit:D'accord, pas de problème ! Merci quand même

Donc tu as trouvé la solution
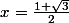
?
-
artichaud
- Membre Naturel
- Messages: 14
- Enregistré le: 29 Oct 2013, 14:15
-
 par artichaud » 01 Nov 2013, 15:27
par artichaud » 01 Nov 2013, 15:27
Carpate a écrit:Donc tu as trouvé la solution
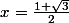
?
Oui, j'ai trouvé deux solutions, soient :
* (1 +

3)/2
* (1 -

3)/2
Mais seule la première solution ((1 +

3)/2) est possible car elle est positive, est-ce ça ?

-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 01 Nov 2013, 18:25
par Carpate » 01 Nov 2013, 18:25
artichaud a écrit:Oui, j'ai trouvé deux solutions, soient :
* (1 +

3)/2
* (1 -

3)/2
Mais seule la première solution ((1 +

3)/2) est possible car elle est positive, est-ce ça ?

Oui, c'est ça
-
artichaud
- Membre Naturel
- Messages: 14
- Enregistré le: 29 Oct 2013, 14:15
-
 par artichaud » 01 Nov 2013, 22:50
par artichaud » 01 Nov 2013, 22:50
Carpate a écrit:Oui, c'est ça
Oh génial ! Après vérification .... ça marche !

Merci beaucoup de ton aide, et celui des autres aussi mais bon voilà ... C'est cool ! Merci

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 90 invités
