Cos, sin, tan (pi/8)
21 messages
- Page 1 sur 2 - 1, 2
cos, sin, tan (pi/8)
Je dois trouver cos pi/8, sin(pi/8) et tan(pi/8) tout en sachant que tan=sin/cos
z² = 1+i
z = a + ib
z² = a²-b² + 2iab
a²-b² = 1
2ab = 1
|z²| = |z|²
V2 = |z|²
a²+b² = V2
on a donc :
a²-b² = 1
2ab = 1
a²+b² = V2
2a² = 1 + V2
a² = (1+V2)/2
Or on sait que : z0 = 2^(1/4).e^(i.(Pi/8) = 2^(1/4).(cos(Pi/8) + i.sin(Pi/8)) = ...
a = 2^(1/4).(cos(Pi/8) > 0
2^(1/4).cos(Pi/8) = V((1+V2)/2)
cos(Pi/8) = [V((1+V2)/2)]/2^(1/4)
cos(pi/8)= (V(2+V2))/2
je n'arrive pas pour "sin"..
z² = 1+i
z = a + ib
z² = a²-b² + 2iab
a²-b² = 1
2ab = 1
|z²| = |z|²
V2 = |z|²
a²+b² = V2
on a donc :
a²-b² = 1
2ab = 1
a²+b² = V2
2a² = 1 + V2
a² = (1+V2)/2
Or on sait que : z0 = 2^(1/4).e^(i.(Pi/8) = 2^(1/4).(cos(Pi/8) + i.sin(Pi/8)) = ...
a = 2^(1/4).(cos(Pi/8) > 0
2^(1/4).cos(Pi/8) = V((1+V2)/2)
cos(Pi/8) = [V((1+V2)/2)]/2^(1/4)
cos(pi/8)= (V(2+V2))/2
je n'arrive pas pour "sin"..
victen a écrit:Je dois trouver cos pi/8, sin(pi/8) et tan(pi/8) tout en sachant que tan=sin/cos
z² = 1+i
z = a + ib
z² = a²-b² + 2iab
a²-b² = 1
2ab = 1
|z²| = |z|²
V2 = |z|²
a²+b² = V2
on a donc :
a²-b² = 1
2ab = 1
a²+b² = V2
2a² = 1 + V2
a² = (1+V2)/2
Or on sait que : z0 = 2^(1/4).e^(i.(Pi/8) = 2^(1/4).(cos(Pi/8) + i.sin(Pi/8)) = ...
a = 2^(1/4).(cos(Pi/8) > 0
2^(1/4).cos(Pi/8) = V((1+V2)/2)
cos(Pi/8) = [V((1+V2)/2)]/2^(1/4)
cos(pi/8)= (V(2+V2))/2
je n'arrive pas pour "sin"..
mais tu trouves quand même le bon résultat ...
Salut !
1°) = 2cos^2 (a)-1) donc pour
donc pour 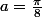 ,
,  = 2cos^2 \( \frac{\pi} 8 \) -1) donc sachant que
donc sachant que  > 0) , tu en déduis
, tu en déduis =...) .
.
2°)=2 \cos (a) \sin (a)) donc pour
donc pour 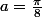 ,
, = \frac{\sin\( \frac{\pi} 4 \)}{2\cos\( \frac{\pi} 8 \)}=...)
:+++:
1°)
2°)
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
21 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
