coucou
alors voila j'ai un dm j'ai plutôt réussi le début mais je n'arrive pas à faire les 2 dernières questions de l'exo
Généralisation
On va supposer que les notes du second élève sont des nombres quelconques a,b,c,d .
8.déterminer l'expression de g(x) , la moyenne des carrés des écarts entre chacune des notes et la valeur fixée .
9. simplifier l'expression de g(x) .
j'ai fait pour la 8:
g(x)= 1/4 ( (x-a)^2 +(x-b)^2 +(x-c)^2 +(x-d)^2 )
pour la 9 :
g(x)= 1/4 ( (x-a)^2 +(x-b)^2 +(x-c)^2 +(x-d)^2 )
=1/4( ( x^2-2ax+ a^2+ x^2-2bx+b^2+ x^2-2cx +c^2+x^2-2dx+d^2 )
=1/4((4x^2 -2(a+b+c+d)x +(a^2+b^2+c^2+d^2))
=x^2 -(a+b+c+d)x/2 + (a^2+b^2+c^2+d^2)/4
est-ce que vous pourrez me dire si c'est juste
maintenant voilà les questions auxquelles je bloque:
10-dresser le tableau de variation de la fonction g.
je l'ai fait mais pour le x j'ai trouvé a+b+c+d x/2 /2
et pour la valeur de g(x) a+b+c+d)x/2-4(a^2+b^2+c^2+d^2)/4 /4
ensuite la 11 déterminer la valeur de x pour laquelle la fonction g atteint son minimum . Que représente cette valeur ?
Quel est alors le minimum de la fonction g
voilà :id:
Dm de maths première
9 messages
- Page 1 sur 1
Hello,
Ce que tu as fait pour les deux première questions me paraît tout à fait correct :zen: .
Pour le 10, j'ai ça comme dérivée de g(x) : = 2x - \frac{a + b + c + d}{2}) .
.
Il y a une racine : .
.
Comme g'(x) est une fonction croissante, g'(x) 0 pour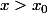 . Ainsi,
. Ainsi, est une minimum de g(x).
est une minimum de g(x).
Après, il reste à calculer ce minimum.
En espérant t'avoir un peu éclairé,
Nerra
Ce que tu as fait pour les deux première questions me paraît tout à fait correct :zen: .
Pour le 10, j'ai ça comme dérivée de g(x) :
Il y a une racine :
Comme g'(x) est une fonction croissante, g'(x) 0 pour
Après, il reste à calculer ce minimum.
En espérant t'avoir un peu éclairé,
Nerra
Nerra a écrit:Hello,
Ce que tu as fait pour les deux première questions me paraît tout à fait correct :zen: .
Pour le 10, j'ai ça comme dérivée de g(x) :.
Il y a une racine :.
Comme g'(x) est une fonction croissante, g'(x) 0 pour. Ainsi,
est une minimum de g(x).
Après, il reste à calculer ce minimum.
En espérant t'avoir un peu éclairé,
Nerra
merci de m'avoir répondu
pour la 10 j'ai un peu compris ce que tu veu dire mais je ne sais pas c'est quoi la dérivée donc je suis un peu perdue :doh:
Ah ... pas de dérivée ... mince ... et désolé  .
.
Alors on va se servir de ce que l'on connaît sur les fonctions du second degré.
Je réécris juste g(x) pour qu'on l'ait devant les yeux, plus facile.
 = x^2 - \frac{(a+b+c+d)x}{2} + \frac{a^2+b^2+c^2+d^2}{4})
Le graphe d'une fonction du second degré est une parabole. On sait que lorsque le coefficient de est positif, la parabole admet un minimum, son sommet. Ici, ce coefficient est 1.
est positif, la parabole admet un minimum, son sommet. Ici, ce coefficient est 1.
S'il était négatif, le sommet de la parabole serait son maximum.
On sait également que les coordonnées du sommet d'une parabole d'équation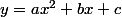 sont
sont ) .
.
Ainsi, la fonction g atteint son minimum en . Fort heureusement, c'est la même réponse que j'avais donnée avant :zen: .
. Fort heureusement, c'est la même réponse que j'avais donnée avant :zen: .
En résumé, ce que tu avais fait était correct, c'est juste qu'il ne faut pas prendre le x, juste le coefficient de x. Tu verras que tu obtiens bien la bonne réponse. La valeur du minimum de g, tu vas l'obtenir sans problème, j'en suis sûr.
Encore désolé pour la réponse à côté de la plaque.
Alors on va se servir de ce que l'on connaît sur les fonctions du second degré.
Je réécris juste g(x) pour qu'on l'ait devant les yeux, plus facile.
Le graphe d'une fonction du second degré est une parabole. On sait que lorsque le coefficient de
S'il était négatif, le sommet de la parabole serait son maximum.
On sait également que les coordonnées du sommet d'une parabole d'équation
Ainsi, la fonction g atteint son minimum en
En résumé, ce que tu avais fait était correct, c'est juste qu'il ne faut pas prendre le x, juste le coefficient de x. Tu verras que tu obtiens bien la bonne réponse. La valeur du minimum de g, tu vas l'obtenir sans problème, j'en suis sûr.
Encore désolé pour la réponse à côté de la plaque.
alors svp quelqu'un pourrait m'aider je n'arrive pas et il me reste que 2 questions
10-dresser le tableau de variation de la fonction g.
ensuite la 11 déterminer la valeur de x pour laquelle la fonction g atteint son minimum . Que représente cette valeur ?
Quel est alors le minimum de la fonction g
voilà, merci
10-dresser le tableau de variation de la fonction g.
ensuite la 11 déterminer la valeur de x pour laquelle la fonction g atteint son minimum . Que représente cette valeur ?
Quel est alors le minimum de la fonction g
voilà, merci
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
