Voici donc l'exercice :
On nous précise que l'on va travailler autour du centre de gravité d'un triangle.
Voici la figure (excusez pour la qualité...) :
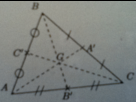
Voici d'abord l'énoncé :
1. Justifiez l'existence de deux réels xG et yG tels que AG = xG*AC + yG*AB (Tous sont des vecteurs).
2. Déterminez les coordonnées de CC' et BB' (vecteurs) dans le repère (A,B,C).
3. En déduire des équations cartésiennes des droites (CC') et (BB').
4. En déduire la valeur de xG et yG.
5. Conclure que AG = 2/3 AA' (vecteurs).
6. Décomposez BG à l'aide de BA et BC. (vecteurs)
7. Décomposez CG à l'aide de CA et CB. (vecteurs)
8. Conclure que GA+GB+GC = 0 (Vecteurs).
Mon avancement dans ce travail :
A vrai dire, je me dessèche...
Le détail qui me pose le plus de problème étant que l'on ne me donne aucune coordonnées sous forme algébrique...
Pour la 1. j'ai pensé à Chasles, mais je ne vois pas du tout comment appliquer dans le cas présent...
Pour la 2. je suppose qu'il me faut d'abord faire la 1.
Pour la 3. Egalement.
Pour la 4. je sais (en fouillant un peu partout) que xG = 1/3 (xA+xB+xC)
yG = 1/3 (yA+yB+yC)
Pour la 5. Etant donné que le centre de gravité d'un triangle est situé à 1/3 d'une médiane par rapport à sa base, alors il est situé à 2/3 de la médiane par rapport à son sommet, donc AG = 2/3 AA' (Je pense que c'est formuler très maladroitement, il faut que je revois ça)
Pour la 6. Il faut décomposé un vecteur avec deux autres vecteurs précis, je me suis penché que très rapidement sur cette question, je la trouve un peu difficile mais une fois que j'ai le départ de Chasles je sais comment faire...
Pour la 7. c'est la même chose...
Pour la 8. Aucun problème.
Comme vous pouvez le voir, ce sont essentiellement les premières questions qui me posent un gros problème...
Merci, et bonne soirée.
