Bloqué sur mon DM

[nyce]

impossible de calculer 8"racine de 3" diviser par 2(9+4"racine de 3")
pourtant la racine est bien positive

[nyce]

Et une autre chose que je n'avais pas tres bien compris c'est comment passer de c²+(t*(t "racine carré"3)/2)/2 (mon résulat) à A(x)=\frac{x^2}{16}+\frac{\sqrt{3}(1-x)^2}{36}

[Tiruxa]

Pourquoi est ce impossible à calculer ? Si c'est le dénominateur irrationnel qui te gène utilise l'expression conjuguée 9-4(racine de 3) et tu obtiendras le résultat que j'avais donné au début (1er message)

[Tiruxa]

parce que c= x/4 et t=y/3=(1-x)/3

[nyce]

Non ce n'est pas le bon résultat.

On a dit plus haut qu'il y a une erreur dans A(x).

A(x,y)=


[/TEX]

C'est pas plutot y² ?

[busard_des_roseaux]

bonjour,


le côté du carré est
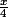
son aire est

le coté du triangle est
son aire est

on doit rendre minimum

9x16=144




on doit minimiser


il n'y a plus de fraction, tu développes, puis forme canonique.

[Tiruxa]

Oui en effet Nyce on voyait bien sûr que c'était y² puisqu'à la ligne au dessous il y avait (1-x)².... je devrais me relire..