Triangle
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
mimouna
- Membre Naturel
- Messages: 21
- Enregistré le: 26 Oct 2013, 10:32
-
 par mimouna » 26 Oct 2013, 11:09
par mimouna » 26 Oct 2013, 11:09
Voici mon énonce avec mon travail qui a besoin d'une correction ^^
Merci d'avance
Triangle 

-
keofran
- Membre Relatif
- Messages: 125
- Enregistré le: 12 Oct 2013, 00:39
- Localisation: Lyon
-
 par keofran » 26 Oct 2013, 12:12
par keofran » 26 Oct 2013, 12:12
Le raisonnement est bon, mais il y a quelques erreurs de notations et surtout la formule du cosinus c'est côté adj / hypo et le sinus c'est côté opp / hypo.

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 26 Oct 2013, 13:44
par chan79 » 26 Oct 2013, 13:44
essayer Al Kashi dans ODF
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 26 Oct 2013, 15:56
par Carpate » 26 Oct 2013, 15:56
keofran a écrit:Le raisonnement est bon, mais il y a quelques erreurs de notations et surtout la formule du cosinus c'est côté adj / hypo et le sinus c'est côté opp / hypo.
Comment peux-tu trouver DF = 50 alors qu'a vue de nez DF est notoirement inférieur au rayon du cercle de rayon 50 cm
l faut savoir (ou du moins retrouver en 2 coups de cuillère à pot) que la hauteur d'un triangle équilatéral de côté a est

Dans l'un des 2 (au choix) triangles rectangles qui s'appuie contre cette hauteur, on sort Pythagore de son tombeau :
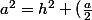^2)


Donc

mais



a~38,5

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 26 Oct 2013, 16:13
par chan79 » 26 Oct 2013, 16:13
Carpate a écrit:Comment peux-tu trouver DF = 50 alors qu'a vue de nez DF est notoirement inférieur au rayon du cercle de rayon 50 cm
l faut savoir (ou du moins retrouver en 2 coups de cuillère à pot) que la hauteur d'un triangle équilatéral de côté a est

Dans l'un des 2 (au choix) triangles rectangles qui s'appuie contre cette hauteur, on sort Pythagore de son tombeau :
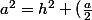^2)


Donc

mais



a~38,5
OH n'est pas égal à R
OD est égal à R/2
je trouve 26.76...
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 26 Oct 2013, 16:29
par Carpate » 26 Oct 2013, 16:29
chan79 a écrit:OH n'est pas égal à R
OD est égal à R/2
je trouve moins ...
26.76...
Toutes mes excuses : tu as raison, j'ai été trompé par la proximité de H avec le cercle ....
Il te faut quand même démontrer que OD = R/2 ce n'est pas bien difficile
Je te conseille dans tes calculs de garder le symbole R jusqu'à la fin et de ne le remplacer par sa valeur qu'à la dernière ligne du calcul

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 26 Oct 2013, 17:36
par chan79 » 26 Oct 2013, 17:36
Carpate a écrit:Je te conseille dans tes calculs de garder le symbole R jusqu'à la fin et de ne le remplacer par sa valeur qu'à la dernière ligne du calcul
Bien-sûr; mais on va laisser à mimouna le plaisir de chercher un peu
-
mimouna
- Membre Naturel
- Messages: 21
- Enregistré le: 26 Oct 2013, 10:32
-
 par mimouna » 26 Oct 2013, 18:03
par mimouna » 26 Oct 2013, 18:03
Bonsoir,
Tout d'abord merci de votre aide ^^.
Est-ce-que je peux le prouver ainsi:
Dans un triangle équilatéral, le centre du cercle circonscrit est aussi le centre circonscrit est aussi le centre de gravité du triangle (pts d'intersection des médianes) et le rayon du cercle est donc égale à deux tiers de la hauteur (d'après la propriété du centre de gravité)
donc*:
R=2/3 CD
50=2/3CD
CD=75
DH=CH-CD
=2*R-75
=2*50-75
=25
Merci ^^
-
mimouna
- Membre Naturel
- Messages: 21
- Enregistré le: 26 Oct 2013, 10:32
-
 par mimouna » 26 Oct 2013, 18:07
par mimouna » 26 Oct 2013, 18:07
Carpate a écrit:Comment peux-tu trouver DF = 50 alors qu'a vue de nez DF est notoirement inférieur au rayon du cercle de rayon 50 cm
l faut savoir (ou du moins retrouver en 2 coups de cuillère à pot) que la hauteur d'un triangle équilatéral de côté a est

Dans l'un des 2 (au choix) triangles rectangles qui s'appuie contre cette hauteur, on sort Pythagore de son tombeau :
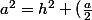^2)


Donc

mais



a~38,5
Pourriez-vous m'expliquer s'il vous plait je n'ai pas compris la démarche :/
Merci ^^
 par busard_des_roseaux » 26 Oct 2013, 18:08
par busard_des_roseaux » 26 Oct 2013, 18:08
bonjour,
H n'appartient pas au cercle.
Il est conseillé d'appliquer Al-Kashi dans le triangle ODF
-
mimouna
- Membre Naturel
- Messages: 21
- Enregistré le: 26 Oct 2013, 10:32
-
 par mimouna » 26 Oct 2013, 18:09
par mimouna » 26 Oct 2013, 18:09
busard_des_roseaux a écrit:bonjour,
H n'appartient pas au cercle.
Il est conseillé d'appliquer Al-Kashi dans le triangle ODF
Oui mais pourriez-vous m'indiquer une autre méthode car je n'ai pas vu cela en classe. ^^
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 26 Oct 2013, 18:11
par Carpate » 26 Oct 2013, 18:11
mimouna a écrit:Bonsoir,
Tout d'abord merci de votre aide ^^.
Est-ce-que je peux le prouver ainsi:
Dans un triangle équilatéral, le centre du cercle circonscrit est aussi le centre circonscrit est aussi le centre de gravité du triangle (pts d'intersection des médianes) et le rayon du cercle est donc égale à deux tiers de la hauteur (d'après la propriété du centre de gravité)
donc*:
R=2/3 CD
50=2/3CD
CD=75
DH=CH-CD
=2*R-75
=2*50-75
=25
Merci ^^
"centre du cercle circonscrit est aussi le centre circonscrit" ??
Qu'est-ce qu'un centre circonscrit ?
"DH=CH-CD
DH=2*R-75"
CH n'est pas égal à 2R, H n'est pas sur le cercle ...
 par busard_des_roseaux » 26 Oct 2013, 18:25
par busard_des_roseaux » 26 Oct 2013, 18:25
as tu vu le produit scalaire ?
si oui, calculer
^2)
de deux manières pour déterminer

-
mimouna
- Membre Naturel
- Messages: 21
- Enregistré le: 26 Oct 2013, 10:32
-
 par mimouna » 26 Oct 2013, 19:31
par mimouna » 26 Oct 2013, 19:31
busard_des_roseaux a écrit:as tu vu le produit scalaire ?
si oui, calculer
^2)
de deux manières pour déterminer

Non :/ Il n'en existe pas une autre méthode?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 26 Oct 2013, 19:36
par chan79 » 26 Oct 2013, 19:36
Pythagore dans OHF, ça va aussi
Tu tombes sur une équation du second degré en a
-
mimouna
- Membre Naturel
- Messages: 21
- Enregistré le: 26 Oct 2013, 10:32
-
 par mimouna » 26 Oct 2013, 20:54
par mimouna » 26 Oct 2013, 20:54
chan79 a écrit:Pythagore dans OHF, ça va aussi
Tu tombes sur une équation du second degré en a
J'ai suivi vos conseils a plusieurs reprises aux brouillons mais je n'arrive pas à trouver 0H pour calculer DH
 par busard_des_roseaux » 26 Oct 2013, 22:48
par busard_des_roseaux » 26 Oct 2013, 22:48
mimouna a écrit:J'ai suivi vos conseils a plusieurs reprises aux brouillons mais je n'arrive pas à trouver 0H pour calculer DH
OH=OD+DH


où c est la longueur du côté du grand (triangle)

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 27 Oct 2013, 07:01
par chan79 » 27 Oct 2013, 07:01
OD=25
OF=50
Pythagore dans OHF
Il faut résoudre
^2+(\fra{a}{2})^2=50^2)
-
mimouna
- Membre Naturel
- Messages: 21
- Enregistré le: 26 Oct 2013, 10:32
-
 par mimouna » 27 Oct 2013, 08:53
par mimouna » 27 Oct 2013, 08:53
busard_des_roseaux a écrit:OH=OD+DH


où c est la longueur du côté du grand (triangle)
Merci pour votre réponse mais OD ne vaut-il pas 1/2R et donc 25 ?
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 27 Oct 2013, 09:04
par beagle » 27 Oct 2013, 09:04
mimouna a écrit:Merci pour votre réponse mais OD ne vaut-il pas 1/2R et donc 25 ?
oui, OD=25 est le 25 que tu vois dans l'équation de Chan qui est Pythagore dans le triangle OHF,
comme il te l'a dit depuis hier!
Et Chan s'est réveillé ce matin tot pour te mettre un message à 07h01mn, alors respect!
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités

