Bonjour, pourriez-vous m'aider à résoudre cette question s'il vous plaît ?
Déterminer la valeur exacte du périmètre d'un double-octaèdre régulier inscrit dans un cercle de rayon 1.
Je sais qu'un double-octaèdre régulier est un polygone régulier à 16 côtés.
Merci d'avance.
Racine carrée
12 messages
- Page 1 sur 1
Hello,
J'ai un petit souci avec l'énoncé. Un octaèdre est un polyèdre à 8 faces, c'est-à-dire une forme géométrique à trois dimensions. Or ici, tu m'as l'air de travailler dans le plan, avec des figures géométriques à deux dimensions, j'ai nommé messieurs les polygones.
Je suppose que tu veux parler d'octogone ? Et que par double-octogone régulier, tu entends un hexadécagone régulier (c'est le petit nom d'un polygone régulier à 16 côtés ou 16-gone).
Nerra
J'ai un petit souci avec l'énoncé. Un octaèdre est un polyèdre à 8 faces, c'est-à-dire une forme géométrique à trois dimensions. Or ici, tu m'as l'air de travailler dans le plan, avec des figures géométriques à deux dimensions, j'ai nommé messieurs les polygones.
Je suppose que tu veux parler d'octogone ? Et que par double-octogone régulier, tu entends un hexadécagone régulier (c'est le petit nom d'un polygone régulier à 16 côtés ou 16-gone).
Nerra
Nerra a écrit:Hello,
J'ai un petit souci avec l'énoncé. Un octaèdre est un polyèdre à 8 faces, c'est-à-dire une forme géométrique à trois dimensions. Or ici, tu m'as l'air de travailler dans le plan, avec des figures géométriques à deux dimensions, j'ai nommé messieurs les polygones.
Je suppose que tu veux parler d'octogone ? Et que par double-octogone régulier, tu entends un hexadécagone régulier (c'est le petit nom d'un polygone régulier à 16 côtés ou 16-gone).
Nerra
Merci pour ta réponse.
Dans mon énoncé on me dit bien un " DOUBLE-OCTAEDRE " en me précisant que c'est un polygone régulier à 16 côtés.
Si on te précise que c'est un polygone, alors parfait mais il n'en reste pas moins qu'un octaèdre n'est pas un polygone. Tu peux vérifier sur Google si tu veux :lol3: .
Et malheureusement, je suis comme siger, j'aurais utilisé quelque chose de ressemblant.
As-tu déjà vu la trigonométrie ? Connais-tu certaines propriétés des polygones réguliers comme leur angle au centre ?
Et malheureusement, je suis comme siger, j'aurais utilisé quelque chose de ressemblant.
As-tu déjà vu la trigonométrie ? Connais-tu certaines propriétés des polygones réguliers comme leur angle au centre ?
Nerra a écrit:Si on te précise que c'est un polygone, alors parfait mais il n'en reste pas moins qu'un octaèdre n'est pas un polygone. Tu peux vérifier sur Google si tu veux :lol3: .
Et malheureusement, je suis comme matheu30, j'aurais utilisé quelque chose de ressemblant.
As-tu déjà vu la trigonométrie ? Connais-tu certaines propriétés des polygones réguliers comme leur angle au centre ?
Oui j'ai déjà vus la trigonométrie mais par contre je ne connais pas la propriété de l'angle au centre. Pourrais-tu m'expliquer s'il te plaît ?
Merci d'avance.
Si tu as déjà vu la trigonométrie, on va pouvoir faire des choses :zen: .
La propriété de l'angle au centre n'a rien de bien terrifiant, tu vas voir.
Imagine-toi, ou dessine, un 16-gone régulier inscrit dans un cercle de rayon 1. Son centre est également le centre du cercle et ses sommets sont sur le cercle. Ainsi, les arêtes du 16-gone sont des rayons du cercle et sont de longueur 1. Le 16-gone est maintenant formé de triangles tous isométriques, ce qui implique que leurs angles sont deux à deux égaux. En particulier, les angles au centre, c'est-à-dire les angles qui sont formés par deux arêtes consécutives, sont d'amplitude .
.
Maintenant, le périmètre du 16-gone. En gros, dans un des triangles considérés, appelons-le A, ci-dessus, si on connaît la longueur du côté opposé à l'angle au centre, on connaît le périmètre du 16-gone, il sera égal à 16 fois la longueur de ce côté. Tout cela est encore justifié par le fait que ces triangles sont isométriques.
Pour ça, on va introduire une autre notion sur les polygones, celle d'apothème. C'est la hauteur d'un triangle issue du centre du 16-gone. A partir de là, il faut faire jouer la trigonométrie avec Pythagore.
Le triangle A est ainsi divisé en deux triangles rectangles isométriques. Tu connais la longueur de l'hypoténuse et tu connais les angles. Repère quelle longueur de côté tu souhaites avoir, calcule-la et n'oublie pas de la multiplier par 2 pour avoir la longueur totale du côté du triangle A.
Ensuite, il ne te reste qu'à multiplier ton résultat par 16 pour avoir le périmètre du 16-gone.
Bien sûr, ce serait plus facile avec un dessin :lol3: .
AJOUT : j'ai failli oublier : travaille en radian, en trigo, c'est obligatoire :marteau:
J'espère t'avoir aidé et si y a encore un souci, hésite pas.
Nerra
La propriété de l'angle au centre n'a rien de bien terrifiant, tu vas voir.
Imagine-toi, ou dessine, un 16-gone régulier inscrit dans un cercle de rayon 1. Son centre est également le centre du cercle et ses sommets sont sur le cercle. Ainsi, les arêtes du 16-gone sont des rayons du cercle et sont de longueur 1. Le 16-gone est maintenant formé de triangles tous isométriques, ce qui implique que leurs angles sont deux à deux égaux. En particulier, les angles au centre, c'est-à-dire les angles qui sont formés par deux arêtes consécutives, sont d'amplitude
Maintenant, le périmètre du 16-gone. En gros, dans un des triangles considérés, appelons-le A, ci-dessus, si on connaît la longueur du côté opposé à l'angle au centre, on connaît le périmètre du 16-gone, il sera égal à 16 fois la longueur de ce côté. Tout cela est encore justifié par le fait que ces triangles sont isométriques.
Pour ça, on va introduire une autre notion sur les polygones, celle d'apothème. C'est la hauteur d'un triangle issue du centre du 16-gone. A partir de là, il faut faire jouer la trigonométrie avec Pythagore.
Le triangle A est ainsi divisé en deux triangles rectangles isométriques. Tu connais la longueur de l'hypoténuse et tu connais les angles. Repère quelle longueur de côté tu souhaites avoir, calcule-la et n'oublie pas de la multiplier par 2 pour avoir la longueur totale du côté du triangle A.
Ensuite, il ne te reste qu'à multiplier ton résultat par 16 pour avoir le périmètre du 16-gone.
Bien sûr, ce serait plus facile avec un dessin :lol3: .
AJOUT : j'ai failli oublier : travaille en radian, en trigo, c'est obligatoire :marteau:
J'espère t'avoir aidé et si y a encore un souci, hésite pas.
Nerra
Nerra a écrit:Si tu as déjà vu la trigonométrie, on va pouvoir faire des choses :zen: .
La propriété de l'angle au centre n'a rien de bien terrifiant, tu vas voir.
Imagine-toi, ou dessine, un 16-gone régulier inscrit dans un cercle de rayon 1. Son centre est également le centre du cercle et ses sommets sont sur le cercle. Ainsi, les arêtes du 16-gone sont des rayons du cercle et sont de longueur 1. Le 16-gone est maintenant formé de triangles tous isométriques, ce qui implique que leurs angles sont deux à deux égaux. En particulier, les angles au centre, c'est-à-dire les angles qui sont formés par deux arêtes consécutives, sont d'amplitude.
Maintenant, le périmètre du 16-gone. En gros, dans un des triangles considérés, appelons-le A, ci-dessus, si on connaît la longueur du côté opposé à l'angle au centre, on connaît le périmètre du 16-gone, il sera égal à 16 fois la longueur de ce côté. Tout cela est encore justifié par le fait que ces triangles sont isométriques.
Pour ça, on va introduire une autre notion sur les polygones, celle d'apothème. C'est la hauteur d'un triangle issue du centre du 16-gone. A partir de là, il faut faire jouer la trigonométrie avec Pythagore.
Le triangle A est ainsi divisé en deux triangles rectangles isométriques. Tu connais la longueur de l'hypoténuse et tu connais les angles. Repère quelle longueur de côté tu souhaites avoir, calcule-la et n'oublie pas de la multiplier par 2 pour avoir la longueur totale du côté du triangle A.
Ensuite, il ne te reste qu'à multiplier ton résultat par 16 pour avoir le périmètre du 16-gone.
Bien sûr, ce serait plus facile avec un dessin :lol3: .
AJOUT : j'ai failli oublier : travaille en radian, en trigo, c'est obligatoire :marteau:
J'espère t'avoir aidé et si y a encore un souci, hésite pas.
Nerra
Merci beaucoup.
Je regarderai ça demain.
bonjour
"double octaèdre" n'est pas un vocabulaire approprié.
Il faudrait que tu regardes comment s'écrit seize en grec et tu rajoutes
le suffixe "gone" derrière.
tu auras besoin de)
à calculer avec le cosinus de l'arc double, via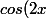=2cos^2(x)-1)
"double octaèdre" n'est pas un vocabulaire approprié.
Il faudrait que tu regardes comment s'écrit seize en grec et tu rajoutes
le suffixe "gone" derrière.
tu auras besoin de
à calculer avec le cosinus de l'arc double, via
Nerra a écrit:Si tu as déjà vu la trigonométrie, on va pouvoir faire des choses :zen: .
La propriété de l'angle au centre n'a rien de bien terrifiant, tu vas voir.
Imagine-toi, ou dessine, un 16-gone régulier inscrit dans un cercle de rayon 1. Son centre est également le centre du cercle et ses sommets sont sur le cercle. Ainsi, les arêtes du 16-gone sont des rayons du cercle et sont de longueur 1. Le 16-gone est maintenant formé de triangles tous isométriques, ce qui implique que leurs angles sont deux à deux égaux. En particulier, les angles au centre, c'est-à-dire les angles qui sont formés par deux arêtes consécutives, sont d'amplitude.
Maintenant, le périmètre du 16-gone. En gros, dans un des triangles considérés, appelons-le A, ci-dessus, si on connaît la longueur du côté opposé à l'angle au centre, on connaît le périmètre du 16-gone, il sera égal à 16 fois la longueur de ce côté. Tout cela est encore justifié par le fait que ces triangles sont isométriques.
Pour ça, on va introduire une autre notion sur les polygones, celle d'apothème. C'est la hauteur d'un triangle issue du centre du 16-gone. A partir de là, il faut faire jouer la trigonométrie avec Pythagore.
Le triangle A est ainsi divisé en deux triangles rectangles isométriques. Tu connais la longueur de l'hypoténuse et tu connais les angles. Repère quelle longueur de côté tu souhaites avoir, calcule-la et n'oublie pas de la multiplier par 2 pour avoir la longueur totale du côté du triangle A.
Ensuite, il ne te reste qu'à multiplier ton résultat par 16 pour avoir le périmètre du 16-gone.
Bien sûr, ce serait plus facile avec un dessin :lol3: .
AJOUT : j'ai failli oublier : travaille en radian, en trigo, c'est obligatoire :marteau:
J'espère t'avoir aidé et si y a encore un souci, hésite pas.
Nerra
Merci beaucoup pour ton explication.
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
