Intégration+séries
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 21 Oct 2013, 20:14
par Sourire_banane » 21 Oct 2013, 20:14
Bonsoir,
J'ouvre ce topic pour les exercices et sujets de concours qui traitent du thème correspondant.
Soit f définie par
=\int_0^1 t^{-x}\sqrt{1+t}\mathrm{d}t)
Le domaine de définition de f est R car la fonction puissance est définie sur R (je me trompe pas ?)
On me demande de donner les variations de f. Pour ce faire, je calcule
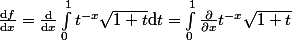\mathrm{d}t=-\int_0^1 \ln t\times t^{-x}\sqrt{1+t}\mathrm{d}t\leq 0)
Encore une fois, ai-je le droit d'écrire ainsi ?
Merci d'avance.

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 21 Oct 2013, 20:40
par fatal_error » 21 Oct 2013, 20:40
slt,
en regardant sur le net, pour pouvoir intervertir dérivée et intégrale, d'apres
futura il faut pouvoir appliquer le théorême de
Leibniz qui dit que ta fonction sous l'intégrale et sa dérivée suivant x doit être continue sur Rx[0,1].
Ici l'intégrande, pad prob
exp(xln(t))*sqrt() sont des produits de fonctions continues et bien définies.
pour les dérivées, ca a l'air good aussi
la vie est une fête

-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 21 Oct 2013, 21:04
par Sourire_banane » 21 Oct 2013, 21:04
fatal_error a écrit:slt,
en regardant sur le net, pour pouvoir intervertir dérivée et intégrale, d'apres
futura il faut pouvoir appliquer le théorême de
Leibniz qui dit que ta fonction sous l'intégrale et sa dérivée suivant x doit être continue sur Rx[0,1].
Ici l'intégrande, pad prob
exp(xln(t))*sqrt() sont des produits de fonctions continues et bien définies.
pour les dérivées, ca a l'air good aussi
Salut fatal_error !
En fait j'ai pas encore vu cette règle en maths mais je l'applique car elle nous est souvent utile en physique. Du coup je sais pas si l'on peut traiter la question par un autre moyen... Enfin je dois sans doute être bête, mais un argument simple sur la décroissance de f1:x->t^{-x} doit suffire pour traiter le pb de la décroissance globale de f. Par contre, je ne vois pas comment le rédiger proprement.
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 21 Oct 2013, 22:44
par Skullkid » 21 Oct 2013, 22:44
Bonsoir, je ne suis pas d'accord avec ton domaine de définition. Par exemple, si tu essayes de calculer f(5), ça donne quoi ?
Ta fonction tombe dans la catégorie de ce qu'on appelle les intégrales à paramètre. Il y a des outils pour les étudier (notamment la règle de Leibniz citée par fatal_error, souvent appelée "dérivation sous le signe intégrale"), mais si tu ne les as pas encore vus, ici tu peux t'en sortir avec la croissance de l'intégrale (si f < g sur I alors int_I(f) < int_I(g)).
Une remarque brachycérophile : en toute rigueur, df/dx est une fonction, pas un nombre. De même, on dérive des fonctions, pas des nombres, donc d(x²+1)/dx, par exemple, ne veut rien dire. Évidemment l'abus de langage à la physicienne est très tentant (et très pratique, et tout le monde l'utilise) mais tant que tu es en apprentissage, évite-le quand tu fais des maths. Sinon tu risques d'être complètement perdu si jamais on t'enseigne du calcul différentiel rigoureusement...
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 22 Oct 2013, 08:52
par jlb » 22 Oct 2013, 08:52
Sourire_banane a écrit:Bonsoir,
J'ouvre ce topic pour les exercices et sujets de concours qui traitent du thème correspondant.
Soit f définie par
=\int_0^1 t^{-x}\sqrt{1+t}\mathrm{d}t)
Le domaine de définition de f est R car la fonction puissance est définie sur R (je me trompe pas ?)
On me demande de donner les variations de f. Pour ce faire, je calcule
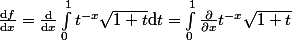\mathrm{d}t=-\int_0^1 \ln t\times t^{-x}\sqrt{1+t}\mathrm{d}t\leq 0)
Encore une fois, ai-je le droit d'écrire ainsi ?
Merci d'avance.
Salut, tu peux préciser pour le signe? pour t dans ]0,1], lnt est négatif, non?
il faut aussi étudier la convergence de la fonction en 0, cela va déterminer le domaine de définition, je crois .
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 22 Oct 2013, 09:16
par jlb » 22 Oct 2013, 09:16
Sourire_banane a écrit:Bonsoir,
J'ouvre ce topic pour les exercices et sujets de concours qui traitent du thème correspondant.
Soit f définie par
=\int_0^1 t^{-x}\sqrt{1+t}\mathrm{d}t)
Le domaine de définition de f est R car la fonction puissance est définie sur R (je me trompe pas ?)
On me demande de donner les variations de f. Pour ce faire, je calcule
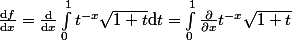\mathrm{d}t=-\int_0^1 \ln t\times t^{-x}\sqrt{1+t}\mathrm{d}t\leq 0)
Encore une fois, ai-je le droit d'écrire ainsi ?
Merci d'avance.
Bonjour, il y a un pb en 0, il faut discuter de la convergence des l'intégrales .
Sinon, un soucis pour le signe, je crois.
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 22 Oct 2013, 14:01
par Sourire_banane » 22 Oct 2013, 14:01
Merci à tous pour vos conseils !
Je regarderai de nouveau ce problème ce soir.
@Skullkid : Ok pour la méthode. Ce pb est issu du second DS des PC*, qui ont suivi à peu près le même programme que nous en maths depuis le début de l'année. Les intégrales à paramètre on a pas vraiment traité ça, et eux non plus d'ailleurs !
Pour le domaine de définition, je croyais qu'en faisant jouer x sur R, l'exponentielle en base t "t^(-x)" serait définie, j'ai tort ?
@jlb : En effet, la nature de f1:t->t^(-x) dépend de x à un voisinage de 0. Auquel cas si x négatif, on a du 1/t^|x|... Si |x|<1, l'intégrale converge car alors on a (1/t^|x|)*sqrt(1+t) equivalent à 1/t^|x| en 0, qui est un exemple de Riemann convergent.
Etc.
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 22 Oct 2013, 17:59
par Skullkid » 22 Oct 2013, 17:59
Sourire_banane a écrit:Pour le domaine de définition, je croyais qu'en faisant jouer x sur R, l'exponentielle en base t "t^(-x)" serait définie, j'ai tort ?
t^(-x) est certes défini pour tout x réel, mais l'intégrale ne va pas forcément converger, comme l'a dit jlb. Le domaine de f est ]-infini,-1[.
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 22 Oct 2013, 18:04
par Sourire_banane » 22 Oct 2013, 18:04
Skullkid a écrit:t^(-x) est certes défini pour tout x réel, mais l'intégrale ne va pas forcément converger, comme l'a dit jlb. Le domaine de f est ]-infini,-1[.
Effectivement, j'ai pas pensé à faire le rapprochement entre convergence de f et valeurs prises par x pour le domaine de définition !
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 25 Oct 2013, 07:49
par deltab » 25 Oct 2013, 07:49
Bonjour.
Résumons un peu tout ça.
t^(-x) est certes défini pour tout x réel, mais l'intégrale ne va pas forcément converger, comme l'a dit jlb. Le domaine de f est ]-infini,-1[.
Ceci a condition que

soit une exponentielle de base

et donc que
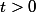
et

. le problème de définition de la fonction

se pose alors aux points
 \in \{0\} \times ]-\infty,0[)
.
Pour
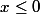
, l'intégrale

est une intégrale définie dépendant d'un paramètre. Comme
=t^{-x} \sqrt{1+t})
est continue sur

, alors la fonction
=\int_0^1 t^{-x} \sqrt{1+t} dt)
est définie continue sur
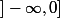
.
Pour

, l'intégrale

est alors une intégrale impropre dépendant d'un paramètre et
)
ne sera définie que si

converge. Vu l'équivalence en
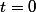
,

, l'intégrale

ne sera convergente que si
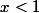
et finalement

-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 25 Oct 2013, 08:14
par jlb » 25 Oct 2013, 08:14
Bonjour, des petits soucis dans les intervalles pour cette synthèse. Mais bon, ce n'est que le début de l'exercice, il reste à justifier la dérivabilité.
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 25 Oct 2013, 08:15
par jlb » 25 Oct 2013, 08:15
Salut. Il reste à justifier la dérivabilité, il y a un peu de boulot aussi!!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
