Équation avec puissance et logarithme.
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
DarkAurora
- Messages: 3
- Enregistré le: 24 Oct 2013, 10:53
-
 par DarkAurora » 24 Oct 2013, 11:02
par DarkAurora » 24 Oct 2013, 11:02
Bonjour, J'ai un problème sur une équation que je n'arrive pas à résoudre:

avec a et b qui sont connus. Il peuvent être remplacer par 20489 pour a et 12 pour b, le résultat étant approximatif.
D'avance merci.
 par busard_des_roseaux » 24 Oct 2013, 11:23
par busard_des_roseaux » 24 Oct 2013, 11:23
bonjour,
l'équation est "transcendante" , il n'y a pas de formule connue pour exprimer la ou les solutions.
Regarder l'intersection des courbes d'équation
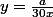
et
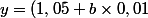^x)
-
DarkAurora
- Messages: 3
- Enregistré le: 24 Oct 2013, 10:53
-
 par DarkAurora » 24 Oct 2013, 12:08
par DarkAurora » 24 Oct 2013, 12:08
Et par approximation? En faite la formule de base est :
energie = ( 30 x Niveau x ( 1,05 + Technologie Energie x 0,01 ) ^ Niveau )
Il s'agit d'une formule permettant de calculer lénergie qu'offre un bâtiment ( pour le jeu Ogame :) )
Je souhaite prendre le problème à l'envers :
Je connais l'énergie dont j'ai besoin mais je veux vérifier si j'ai bien le niveau de bâtiment requis! Or je sais très bien ( si on suppose qu'un résultat est possible ) qu'il ne tombera pas juste en fait mon équation est inexacte elle devrais plutôt être :
energie < ( 30 x Niveau x ( 1,05 + Technologie Energie x 0,01 ) ^ Niveau )
energie & Technologie Energie étant connus et Niveau étant obligatoirement un entier.
-
Dlzlogic
- Membre Transcendant
- Messages: 5273
- Enregistré le: 14 Avr 2009, 12:39
-
 par Dlzlogic » 24 Oct 2013, 12:22
par Dlzlogic » 24 Oct 2013, 12:22
Pour résoudre ce genre de chose, j'utilise généralement la méthode de Newton.
Il y a une autre méthode possible à un certain nombre de conditions.
Supposons que vous connaissiez le domaine de définition (valeur min et valeur max), on calcule une dizaine de valeurs intermédiaires exactes, et on cherche s'il n'y a pas une formule légèrement différente mais suffisamment approchée pour les besoins réels.
-
DarkAurora
- Messages: 3
- Enregistré le: 24 Oct 2013, 10:53
-
 par DarkAurora » 24 Oct 2013, 12:24
par DarkAurora » 24 Oct 2013, 12:24
Merci tu viens de me donner l'idée me permettant de réaliser un script, pas génial mais mieux que rien.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 24 Oct 2013, 12:45
par leon1789 » 24 Oct 2013, 12:45
DarkAurora a écrit:energie < 30 x Niveau x ( 1,05 + Technologie Energie x 0,01 ) ^ Niveau
energie & Technologie Energie étant connus et Niveau étant obligatoirement un entier.
C'est l'entier Niveau qui est inconnu.
Ce n'est pas compliqué de trouver le Niveau minimum : il suffit de tester les entiers 1, 2, ... les uns après les autres. Cela donne un premier algorithme simple (mais peu efficace si le Niveau cherché est gigantesque).
Par ailleurs, Niveau doit inférieur à (sans être loin de)
}{\ln( 1,05 + 0.01 Technologie Energie )})
. On peut partir de
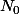
, puis regarder

,

, etc.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités

