Theoreme de fejer
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
stella54
- Membre Naturel
- Messages: 46
- Enregistré le: 06 Jan 2008, 14:07
-
par stella54 » 15 Oct 2013, 23:02
Si f est une fonction réelle (ou complexe) de variable réelle, continue et 2
, on a:
:= \frac{1}{2\pi} \int_{\theta = 0}^{2\pi} f(\theta) \exp^{-ik\theta} d\theta)
(\theta):= \sum_{k=-n}^{n} c(f) \exp^{ik\theta}, D_n(\theta)=\sum_{k=-n}^{n} \exp^{ik\theta})
=\frac{\sum_{k=0}^{N} S_n(f)}{N+1}, F_N=\frac{\sum_{k=0}^{N} D_n}{N+1})
Le but est de le démontrer.
Theoreme: Si f est continue, alors la suite de fonctions
)
converge uniformément vers la
fonction f.
1)a) Montrer que :
=\frac{sin(\frac{(2n+1)\theta}{2})}{sin(\frac{\theta}{2})})
ou
b)
=\frac{1}{N+1}\frac{sin^2(\frac{(2n+1) \theta}{2})}{sin^2(\frac{\theta}{2})})
ou
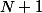
c)
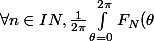 d\theta = 1)
d)
 \leq \frac{1}{(N+1)sin^2(\frac{\delta}{2})})
2)a)
Montrer que:
(\theta)=\frac{1}{2\pi} \int_{\theta = 0}^{2\pi} f(\phi)F_N (\theta-\phi) d\phi = \frac{1}{2\pi} \int_{\theta = 0}^{2\pi} f(\theta-\phi)F_N (\phi) d\phi)
b)Montrer que:
(\theta)-f(\theta)=\frac{1}{2\pi} \int_{\theta = 0}^{2\pi} (f(\theta-\phi)-f(\theta))F_N (\phi) d\phi)
c) Montrer que:
(\theta)-f(\theta) | \leq \frac{1}{2\pi} \int_{\phi = 0}^{2\pi} |f(\theta-\phi)-f(\theta) | F_N (\phi) d\phi)
d) Montrer que:
-f(\theta) | F_N (\phi) d\phi \leq max_{\theta \psi \in IR; | \psi-\theta|\leq \delta |} | f(\psi)-f(\theta) |)
e) Montrer que:
-f(\theta) | F_N (\phi) d\phi \leq \frac{1}{(N+1)sin^2(\frac{\delta}{2})})
f) Conclure
J'ai reussi le 1)a)
pour le 1)b) je voit pas comment faire
-
lionel52
- Membre Relatif
- Messages: 274
- Enregistré le: 21 Nov 2012, 22:39
-
par lionel52 » 15 Oct 2013, 23:45
Tu peux procéder par récurrence !
Sinon pour que ça paraisse moins parachuté (encore que)
La somme des Dn c'est aussi la somme
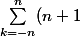e^{i k \theta} - \sum_{k=-n}^n |k| e^{i k \theta})
(il y a n+1-|k| fois le terme en exp(iktheta)
La première somme tu l'as calculée, la 2e c'est presque la dérivée de la 1ere !
Mais en vérité faut séparer en 2 la 2e somme à cause des valeurs absolues
-
stella54
- Membre Naturel
- Messages: 46
- Enregistré le: 06 Jan 2008, 14:07
-
par stella54 » 16 Oct 2013, 00:24
pour la 1)a) c'est bon, Pour la 1)b) je voulais savoir pour calculer
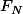
pour
different de 0
J'ai besoin de
)
et
)
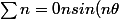\theta}}{1-\exp^{i \theta}})
en utilisant euler:
+i sin(n \theta))
\theta}}{1-\exp^{i \theta}}) <br /><br />\sum_{n=0}^{N} sin{ n \theta}= Partie Imaginaire (\frac{1- \exp^{i(N+1)\theta}}{1-\exp^{i \theta}}))
je trouve donc
\theta}}{1-\exp^{i \theta}})<br /> \\ = \frac{1-cos((N+1)\theta)}{1-cos(\theta)})
c'est sa??
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
par Joker62 » 16 Oct 2013, 06:07
Sans oublier que :
 = \cos^2(x) - \sin^2(x) = 1 - 2\sin^2(x))
Et donc
 = \dfrac{1-\cos(2x)}{2})
-
stella54
- Membre Naturel
- Messages: 46
- Enregistré le: 06 Jan 2008, 14:07
-
par stella54 » 16 Oct 2013, 08:47
déja est-ce que
\theta}}{1-\exp^{i \theta}})= \frac{1-cos((N+1)\theta)}{1-cos(\theta)})
???
\theta}{2})=\frac{1-cos((2n+1)\theta)}{2}<br />sin^2(\frac{\theta}{2})=\frac{1-cos(\theta)}{2})
donc
\theta}{2})}{sin^2(\frac{\theta}{2})}<br /> =\frac{1-cos((2n+1)\theta)}{1-cos(\theta)})
je doit trouver que
\theta)}{1-cos(\theta)})
avec
\theta}{2})}{sin(\frac{\theta}{2})})
mais je voit pas comment?
-
lionel52
- Membre Relatif
- Messages: 274
- Enregistré le: 21 Nov 2012, 22:39
-
par lionel52 » 16 Oct 2013, 09:46
Je sais pas ce que tu fais mais une autre méthode c'est de dire que
} \sum_{k=0}^n Im (e^{i \theta/2} e^{i k \theta})<br />= \frac{1}{sin(\theta/2)} Im( e^{i (n+1)\theta/2}\times \frac{sin((n+1)\theta/2)}{sin(\theta/2)})<br />= \frac{sin^2((n+1)\theta/2)}{sin^2(\theta/2)})
Donc t'as fait une ptite erreur dans l'énoncé!
-
stella54
- Membre Naturel
- Messages: 46
- Enregistré le: 06 Jan 2008, 14:07
-
par stella54 » 16 Oct 2013, 09:49
Pourquoi tu met
})
alors que l'enoncé nous dit
-
lionel52
- Membre Relatif
- Messages: 274
- Enregistré le: 21 Nov 2012, 22:39
-
par lionel52 » 16 Oct 2013, 10:08
je reprends juste l'expression de Dn trouvée dans la 1a. Le n+1 je l'ai pas fait apparaitre
-
stella54
- Membre Naturel
- Messages: 46
- Enregistré le: 06 Jan 2008, 14:07
-
par stella54 » 16 Oct 2013, 10:36
Rectification d'énoncé c'est bien
\theta)}{2})}{sin^2(\frac{\theta}{2})})
-
stella54
- Membre Naturel
- Messages: 46
- Enregistré le: 06 Jan 2008, 14:07
-
par stella54 » 16 Oct 2013, 10:50
} \sum_{k=0}^n Im (e^{i \theta/2} e^{i k \theta})<br /><br />= \frac{1}{sin(\theta/2)} Im( e^{i (n+1)\theta/2}\times \frac{sin((n+1)\theta/2)}{sin(\theta/2)}))
Pourquoi??
Moi je trouve:
=Im(e^{i \theta/2}*\sum_{k=0}^n <br />Im (e^{i k \theta}))
ce qui donne
\theta}}{1-e^{i \theta}}))
-
stella54
- Membre Naturel
- Messages: 46
- Enregistré le: 06 Jan 2008, 14:07
-
par stella54 » 16 Oct 2013, 11:27
c'est bon pour le 1)b) j'ai compris
Maintenant pour le 1)c)
Je trouve
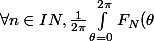 d\theta = \frac{1}{2\pi} \int_{\theta = 0}^{2\pi} \frac{1}{N+1}\frac{sin^2(\frac{(n+1) \theta}{2})}{sin^2(\frac{\theta}{2})} d\theta = \frac{1}{2\pi (N+1)} \int_{\theta = 0}^{2\pi} \frac{sin^2(\frac{(n+1) \theta}{2})}{sin^2(\frac{\theta}{2})} d\theta)
Apres trouver une integrale de sa, c'est compliqué
-
lionel52
- Membre Relatif
- Messages: 274
- Enregistré le: 21 Nov 2012, 22:39
-
par lionel52 » 16 Oct 2013, 13:10
prends la forme la plus simple pour l'intégration :) pas obligé de prendre le quotient horrible de sinus
-
stella54
- Membre Naturel
- Messages: 46
- Enregistré le: 06 Jan 2008, 14:07
-
par stella54 » 16 Oct 2013, 17:01
pour le 1)c)
j'arrive pas à intégré
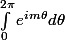
pour m different de 0 je doit trouver 0
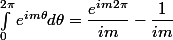
Pourquoi
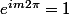
c'est p-etre tt bete mais je voit pas
-
stella54
- Membre Naturel
- Messages: 46
- Enregistré le: 06 Jan 2008, 14:07
-
par stella54 » 16 Oct 2013, 18:40
Pour la d)
Comment je montre
 \leq \frac{1}{(N+1)sin^2(\frac{\delta}{2})})
-
stella54
- Membre Naturel
- Messages: 46
- Enregistré le: 06 Jan 2008, 14:07
-
par stella54 » 16 Oct 2013, 21:43
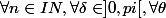
tel que
=\dfrac{1}{N+1}\dfrac{sin^2(\dfrac{(N+1) \theta}{2})}{sin^2(\dfrac{\theta}{2})} <br /><br /> \\ \delta< \theta<2\pi-\delta \\\\<br /> \dfrac{\delta}{2}<\dfrac{\theta}{2}<\dfrac{2\pi-\delta}{2})
si je dit que
 \theta}{2})|<|1|)
 \theta}{2})}{sin^2(\dfrac{\theta}{2})} |< \dfrac{1}{N+1}\dfrac{sin^2(\dfrac{(N+1) \theta}{2})}{sin^2(\dfrac{\theta}{2})} < \dfrac{1}{(N+1) sin^2(\dfrac{\theta}{2})})
c bon??
-
lionel52
- Membre Relatif
- Messages: 274
- Enregistré le: 21 Nov 2012, 22:39
-
par lionel52 » 17 Oct 2013, 10:25
le sin² n'est pas strict inférieur à 1 et tu ne lis pas l'énoncé! tu dois avoir autre chose au dénominateur!
juste une question, tu es dans quel cursus actuellement?
-
stella54
- Membre Naturel
- Messages: 46
- Enregistré le: 06 Jan 2008, 14:07
-
par stella54 » 17 Oct 2013, 12:26
L3
mais il n'y a rien d'autre au dénominateur, il y a que sa
-
lionel52
- Membre Relatif
- Messages: 274
- Enregistré le: 21 Nov 2012, 22:39
-
par lionel52 » 17 Oct 2013, 14:09
lis ton énoncé........................................................... :dodo:
-
stella54
- Membre Naturel
- Messages: 46
- Enregistré le: 06 Jan 2008, 14:07
-
par stella54 » 17 Oct 2013, 16:43
on sait que
> sin(\frac{\delta}{2}))
car sin(x) est croissant entre 0 et
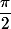
et
> sin(\frac{\theta}{2}))
car sin(x) est décroissant entre
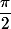
et
=\dfrac{1}{N+1}\dfrac{sin^2(\dfrac{(N+1) \theta}{2})}{sin^2(\dfrac{\theta}{2})}<= \dfrac{1}{N+1}\dfrac{sin^2(\dfrac{(N+1) \delta}{2})}{sin^2(\dfrac{\delta}{2})})
si
est compris entre 0 et
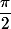
Apres pourquoi le 1 au numérateur
-
stella54
- Membre Naturel
- Messages: 46
- Enregistré le: 06 Jan 2008, 14:07
-
par stella54 » 17 Oct 2013, 22:39
Pour le 2)a)
je doit montrer que
(\theta)=\dfrac{1}{2\pi} \int_{\phi = 0}^{2\pi} f(\phi) F_N (\theta-\phi) d\phi = \dfrac{1}{2\pi} \int_{\phi = 0}^{2\pi} f(\theta-\phi)F_N (\phi) d\phi)
Sachant que:
(\theta)=\dfrac{\sum_{n=0}^{N} S_n(f)}{N+1}<br /> S_n(f)(\theta):= \sum_{k=-n}^{n} c(f) e^{ik\theta})
et
:= \frac{1}{2\pi} \int_{\theta = 0}^{2\pi} f(\theta) e^{-ik\theta} d\theta)
Donc
(\theta)=\dfrac{\sum_{n=0}^{N} S_n(f)}{N+1}=\dfrac{\sum_{k=0}^{N} \sum_{k=-n}^{n} c(f) e^{ik\theta}}{N+1} = \dfrac{\sum_{k=0}^{N} \sum_{k=-n}^{n} \frac{1}{2\pi} \int_{\theta = 0}^{2\pi} f(\theta) e^{-ik\theta} d\theta e^{ik\theta}}{N+1})
Apres comment avoir
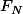
dans
)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
par Pseuda » 03 Avr 2016, 18:28
