soit P(x)=x^3+2x²-27x+36
quelle conjecture peut on faire sur une racine de P?
merci
Conjecture
16 messages
- Page 1 sur 1
par fonfon » 03 Sep 2006, 14:36
Salut,
on a :}=x^3+2x^2-27x+36)
tu remplaces x successivement par des valeurs simples ici tu essaies avec -3,-2,-1,0,1,2,3 et tu regardes avec quelle(s) valeur(s) le polynôme s'annule. En terminale c'est rare qu'une racine evidente soit autre que celles que je t'ai donné, donc ici on remarque que P(3)=0 donc il semble que P(x) soit factorisable par (x-3) (i.e 3 est racine de P(x)).Après à toi de le demontrer
A+
on a :
tu remplaces x successivement par des valeurs simples ici tu essaies avec -3,-2,-1,0,1,2,3 et tu regardes avec quelle(s) valeur(s) le polynôme s'annule. En terminale c'est rare qu'une racine evidente soit autre que celles que je t'ai donné, donc ici on remarque que P(3)=0 donc il semble que P(x) soit factorisable par (x-3) (i.e 3 est racine de P(x)).Après à toi de le demontrer
A+
par haydenstrauss » 03 Sep 2006, 14:58
apres avoir mi x-3 en facteur il faut faire une identification
par Nightmare » 03 Sep 2006, 15:07
Il FAUT faire une identification ? Non, on peut, mais c'est fastidieux.
Il suffit d'écrire P(x)=x²(x-3)+5x²-27x+36=x²(x-3)+(x-3)(5x-12)=(x-3)(x²+5x-12)
:happy3:
Il suffit d'écrire P(x)=x²(x-3)+5x²-27x+36=x²(x-3)+(x-3)(5x-12)=(x-3)(x²+5x-12)
:happy3:
par fonfon » 03 Sep 2006, 15:12
d'accord avec toi Nightmare mais je sais pas si tout le monde à ton coup d'oeuil :++:
par Nightmare » 03 Sep 2006, 18:18
Ce n'est pas une question de vue ou non, la méthode est toujours la même, quelque soit le polynôme.
Ici, on partait de x^3+2x²-27x+36
On a vu que 3 était une racine de ce polynôme, donc qu'il était factorisable par (x-3).
Ainsi, on commence a factoriser le terme du plus haut degré par (x-3) :
x^3=x²(x-3)+3x²
Ainsi le polynôme vaut :
x²(x-3)+5x²-27x+36
Etant donné qu'on a dit qu'il était factorisable par (x-3), c'est que 5x²-27x+36 l'est aussi, donc qu'il existe a et b tels que 5x²-27x+36=(x-3)(ax+b).
L'identification se fait imédiatement de tête, pour que le coefficient en x² soit conservé il faut que a soit égal à 5 et pour que le monôme de degré nul soit conversé il faut que b soit égal à 12. On avait donc 5x²-27x+36=(x-3)(5x+12)
C'est juste un coup de main à prendre.
Exemple, factoriser :
1 est clairement une racine donc (x-1) divise notre polynôme.
On remarque notament que :
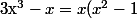=x(x-1)(x+1))
On a fait apparaitre le facteur (x-1), cela veut dire que ce qui n'a pas été factorisé, soit
est divisible par (x-1)
Par chance, c'est un trinôme bicarré.
On sait que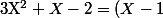(X+2))
d'où finalement :
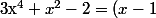(x+1)(x^{2}+2))
Par conséquent :
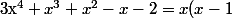(x+1)+(x-1)(x+1)(x^{2}+2)=(x-1)(x+1)(x^{2}+x+2))
Rapide et efficace, on a même fait apparaitre une autre racine :lol3: (c'est encore plus efficace lorsqu'on se dispense de toutes les explications superflues)
:happy3:
Ici, on partait de x^3+2x²-27x+36
On a vu que 3 était une racine de ce polynôme, donc qu'il était factorisable par (x-3).
Ainsi, on commence a factoriser le terme du plus haut degré par (x-3) :
x^3=x²(x-3)+3x²
Ainsi le polynôme vaut :
x²(x-3)+5x²-27x+36
Etant donné qu'on a dit qu'il était factorisable par (x-3), c'est que 5x²-27x+36 l'est aussi, donc qu'il existe a et b tels que 5x²-27x+36=(x-3)(ax+b).
L'identification se fait imédiatement de tête, pour que le coefficient en x² soit conservé il faut que a soit égal à 5 et pour que le monôme de degré nul soit conversé il faut que b soit égal à 12. On avait donc 5x²-27x+36=(x-3)(5x+12)
C'est juste un coup de main à prendre.
Exemple, factoriser :
1 est clairement une racine donc (x-1) divise notre polynôme.
On remarque notament que :
On a fait apparaitre le facteur (x-1), cela veut dire que ce qui n'a pas été factorisé, soit
Par chance, c'est un trinôme bicarré.
On sait que
d'où finalement :
Par conséquent :
Rapide et efficace, on a même fait apparaitre une autre racine :lol3: (c'est encore plus efficace lorsqu'on se dispense de toutes les explications superflues)
:happy3:
par nada-top » 03 Sep 2006, 20:43
et cela sans oublier biensur la méthode de HÖRNER :lol4:
par ex : = x^4)
on peut remarquer que 
est une racine
donc = (x-2)(a_0x^3 + a_1x^2 + a_2x + a_3 ))
on veut trouvé
et 
:
(meme coeficient du 
)
 +)
(
)
 +)
+)
()
ainsi = (x-2) ( x^3 + 5x + 7))
pour notre exemple : = x^3 + 2x^2-27x+36 = (x-3)(a_0x^2 + a_1x+a_2))
ainsi les calculs se font rapidement on obtient = (x-3)(x^2 + 5x -12 ))
par ex :
donc
on veut trouvé
ainsi
pour notre exemple :
ainsi les calculs se font rapidement on obtient
par haydenstrauss » 04 Sep 2006, 10:06
pas mal la methode de HORNER c'est sympa :)
par contre night je trouve pas sa si simple que ta methode mais bon ça donne directement le resultat
par contre night je trouve pas sa si simple que ta methode mais bon ça donne directement le resultat
par Flodelarab » 04 Sep 2006, 10:58
nekros a écrit:Pas mal du tout ce cher Hörner :++:
Ce Hörner ??? Cette Hörner, non ?
J'ai toujours cru que c t Yvette Hörner...
par nada-top » 04 Sep 2006, 11:11
toujours l'humour :ptdr:
heureusement il y a un tréma sur le ''o'' de William HÖRNER , mais pas sur celui d'Yvette.
heureusement il y a un tréma sur le ''o'' de William HÖRNER , mais pas sur celui d'Yvette.
par Flodelarab » 04 Sep 2006, 12:07
ahhhhhhhhhhhhhhhhhh
Merci! Ta précision me permet de découvrir que William Hörner est un mathématicien britannique à cheval sur le XVIIIe et XIXe siècle.
Je me rend compte du peu de point commun avec la virtuose ... (même pas la couleur de cheveux!)
:++:
Merci! Ta précision me permet de découvrir que William Hörner est un mathématicien britannique à cheval sur le XVIIIe et XIXe siècle.
Je me rend compte du peu de point commun avec la virtuose ... (même pas la couleur de cheveux!)
:++:
par Quidam » 04 Sep 2006, 13:18
nada-top a écrit:et cela sans oublier biensur la méthode de HÖRNER
Bien vu ! Voir aussi l'explication de Chimerade sur ce sujet !
http://www.maths-forum.com/showthread.php?t=4888
par nada-top » 04 Sep 2006, 21:11
oui Quidam c'est presque le meme principe à moins que Chimerade a oublié de signaler que cela s'appelle algorithme de HÖRNER :ptdr:
en tous cas je voulais juste ajouter une précision :
le fait que a soit une racine est un cas particulier , cela dit que cet algorithme sert aussi à calculer)
quel que soit le nombre 
avec moins d'opérations.
eg pour l'ex précédent=x^4-2x^3+5x^2-3x-14)
pour calculer 
on s'est servi de tous les termes des des mônomes de P(x) sauf le terme constant (-14) donc à quoi sert ?
voilà = (2\times a_3 ) - 14 = 0})
(on a déjà trouvé 
)
d'une part on est maintenant sur que a=2 est une racine et d'autre part on calcule)
par le moindre des opérations possible .
en général pour tout a (racine ou non), cet algorithme permet de déterminer en meme temps et )
tel que :  - P(a) = (x-a) . Q(x))
en tous cas je voulais juste ajouter une précision :
le fait que a soit une racine est un cas particulier , cela dit que cet algorithme sert aussi à calculer
eg pour l'ex précédent
voilà
d'une part on est maintenant sur que a=2 est une racine et d'autre part on calcule
en général pour tout a (racine ou non), cet algorithme permet de déterminer en meme temps
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :