Reste de série
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
majin
- Membre Naturel
- Messages: 83
- Enregistré le: 12 Nov 2011, 21:30
-
 par majin » 03 Oct 2013, 18:45
par majin » 03 Oct 2013, 18:45
bonsoir, je dois montrer que
}\int_{0}^{1}\frac{x(1-x)}{k+x}dx\leq \frac{1}{12n(n+1)})
j'ai majoré

par
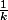
, et
}=\frac{1}{k+1}-\frac{1}{k}+\frac{1}{k^2})
, la premiere somme est télescopique et la deuxième je l'ai majoré par

finalement je trouve que
})
,j'arrive pas à trouver le 2 pour avoir 12
quelqu'un a une idée pour une majoration plus fine? Merci
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 03 Oct 2013, 19:39
par Sourire_banane » 03 Oct 2013, 19:39
majin a écrit:bonsoir, je dois montrer que
}\int_{0}^{1}\frac{x(1-x)}{k+x}dx\leq \frac{1}{12n(n+1)})
j'ai majoré

par
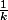
, et
}=\frac{1}{k+1}-\frac{1}{k}+\frac{1}{k^2})
, la premiere somme est télescopique et la deuxième je l'ai majoré par

finalement je trouve que
})
,j'arrive pas à trouver le 2 pour avoir 12
quelqu'un a une idée pour une majoration plus fine? Merci
Salut,
Tu peux trouver un équivalent de la somme (indexée par p) des 1/k² lorsque p devient grand.
Essaie une comparaison série-intégrale.
-
majin
- Membre Naturel
- Messages: 83
- Enregistré le: 12 Nov 2011, 21:30
-
 par majin » 03 Oct 2013, 19:45
par majin » 03 Oct 2013, 19:45
Sourire_banane a écrit:Salut,
Tu peux trouver un équivalent de la somme (indexée par p) des 1/k² lorsque p devient grand.
Essaie une comparaison série-intégrale.
oui j'ai fait une comparaison série- intégrale pour montrer que cette somme est majoré par 1/n, en fait on a même équivalence
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 03 Oct 2013, 19:46
par Sourire_banane » 03 Oct 2013, 19:46
majin a écrit:oui j'ai fait une comparaison série- intégrale pour montrer que cette somme est majoré par 1/n, en fait on a même équivalence
Oui oui je sais, je viens de tester.
Alors tes précédentes majorations sont peut-être un peu grossières ?
Enfin moi je trouve que c'est assez précis pour avoir oublié un facteur 2...
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 04 Oct 2013, 16:17
par deltab » 04 Oct 2013, 16:17
Bonjour
Sourire_banane a écrit:Oui oui je sais, je viens de tester.
Alors tes précédentes majorations sont peut-être un peu grossières ?
Enfin moi je trouve que c'est assez précis pour avoir oublié un facteur 2...
Tu as majoré la fonction f par
})
La majoration la "plus précise" de
=\dfrac{x(1-x)}{k+x})
pour
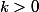
est
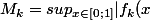|=sup_{x \in [0;1]} f_k(x))
(on sait déjà que

est bornée), mais ceci n'est pas nécessaire. On peut utiliser soit la majoration :
=\dfrac{x(1-x)}{k+x} \le \dfrac{x(1-x)}{k} \le \dfrac{sup_{x \in [0;1]}(x(1-x))}{k}=\dfrac{1}{4k})
(ce qui donnera au final une majoration par
})
soit la majoration:
=\dfrac{x(1-x)}{k+x} \le \dfrac{x(1-x)}{k})
puis
 dx \le \dfrac{1}{k} \int_0^1 x(1-x) dx =\dfrac{1}{k}(\dfrac{1}{2}-\dfrac{1}{3})=\dfrac{1}{6k})
. Ce qui donnera comme majoration finale
})
Les 2 majorations trouvées sont meilleures que celle qu'on à montrer.
Sauf erreur
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 04 Oct 2013, 18:36
par Sourire_banane » 04 Oct 2013, 18:36
deltab a écrit:Bonjour
Tu as majoré la fonction f par
})
La majoration la "plus précise" de
=\dfrac{x(1-x)}{k+x})
pour
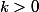
est
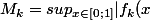|=sup_{x \in [0;1]} f_k(x))
(on sait déjà que

est bornée), mais ceci n'est pas nécessaire. On peut utiliser soit la majoration :
=\dfrac{x(1-x)}{k+x} \le \dfrac{x(1-x)}{k} \le \dfrac{sup_{x \in [0;1]}(x(1-x))}{k}=\dfrac{1}{4k})
(ce qui donnera au final une majoration par
})
soit la majoration:
=\dfrac{x(1-x)}{k+x} \le \dfrac{x(1-x)}{k})
puis
 dx \le \dfrac{1}{k} \int_0^1 x(1-x) dx =\dfrac{1}{k}(\dfrac{1}{2}-\dfrac{1}{3})=\dfrac{1}{6k})
. Ce qui donnera comme majoration finale
})
Les 2 majorations trouvées sont meilleures que celle qu'on à montrer.
Sauf erreur
Salut deltab.
Tu viens de majorer l'intégrale, et tu remarqueras que nous l'avions fait aussi. Majin a bel et bien majoré son intégrale par 6k...
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 04 Oct 2013, 20:36
par deltab » 04 Oct 2013, 20:36
Bonsoir.
Sourire_banane
Tu veux dire par 1/6k, non, il a majoré sa fonction par 1/k et donc l'intégrale aussi par 1/k. Il a bien écrit:
j'ai majoré

, et
}=\frac{1}{k+1}-\frac{1}{k}+\frac{1}{k^2})
La dernière égalité prouve bien qu'il a majoré l'intégrale par 1/k.
e celle de
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 04 Oct 2013, 20:56
par Sourire_banane » 04 Oct 2013, 20:56
deltab a écrit:Bonsoir.
Sourire_banane
Tu veux dire par 1/6k, non, il a majoré sa fonction par 1/k et donc l'intégrale aussi par 1/k. Il a bien écrit:
La dernière égalité prouve bien qu'il a majoré l'intégrale par 1/k.
Oui oui, 1/6k bien sûr.
Et non, parce qu'on avait d'ores et déjà majoré la somme toute entière par celle des 1/(6k²(k+1)), après avoir majoré l'intégrale par 1/6k.
Lis bien, tu verras que Majin avait majoré 1/(x+k) par 1/x, afin de multiplier l'inégalité par la valeur x(1-x) positive, avant de l'intégrer.
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 04 Oct 2013, 21:30
par deltab » 04 Oct 2013, 21:30
Sourire_banane a écrit:Oui oui, 1/6k bien sûr.
Et non, parce qu'on avait d'ores et déjà majoré la somme toute entière par celle des 1/(6k²(k+1)), après avoir majoré l'intégrale par 1/6k.
Lis bien, tu verras que Majin avait majoré 1/(x+k) par 1/x, afin de multiplier l'inégalité par la valeur x(1-x) positive, avant de l'intégrer.
Exact, mais Majin avait majoré 1/(x+k) par 1/k. Comme il n'a pas explicité le facteur 1/6, j'ai cru qu'il provenait de la majoration de la somme. Il est alors évident que les majoration que j'avais déduites sont erronées.
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 06 Oct 2013, 14:29
par deltab » 06 Oct 2013, 14:29
Bonjour.
Il faudra peut-être
calculer et non pas
majorer l'intégrale
}{k+x}dx)
pour en déduire la majoration souhaitée de
} \int_0^1 \dfrac{x(1-x)}{k+x}dx)
-
majin
- Membre Naturel
- Messages: 83
- Enregistré le: 12 Nov 2011, 21:30
-
 par majin » 10 Oct 2013, 18:45
par majin » 10 Oct 2013, 18:45
Je voulais poster la réponse depuis longtemps mais là voici :we:
j'ai majoré

par
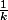
puis par

et on montre que
k(k+1)}=\frac{1}{2n(n+1)})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
}\int_{0}^{1}\frac{x(1-x)}{k+x}dx\leq \frac{1}{12n(n+1)})
par
, et
, la premiere somme est télescopique et la deuxième je l'ai majoré par

,j'arrive pas à trouver le 2 pour avoir 12
pour
est
(on sait déjà que
est bornée), mais ceci n'est pas nécessaire. On peut utiliser soit la majoration :
(ce qui donnera au final une majoration par
puis
. Ce qui donnera comme majoration finale