Exercice suite

[lopilu]

Bonjour/bonsoir à tous !
Me voilà que je bloque sur un exercice sur les suites, simplement car je n'ai pas d'idées pour traiter la question... La voici :

On va étudier la suite définie par et ,
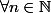
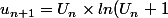Dans la Partie I, on a déjà étudié la suite associée à cette fonction. La question à laquelle je n'arrive pas à démarrer est la suivante :
On suppose dans cette question que .
Montrer que : ,

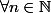
La suite de l'exercice devrait moins me poser de problème, mais je bute sur cette question...
Merci infiniment de votre aide, comme toujours ! :we:

[deltab]

Bonjour

Bonjour/bonsoir à tous !

On suppose dans cette question que .
Montrer que : ,

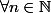
Etudies la fonction et si on a , que peut-on conclure?

[lopilu]

Après avoir étudié la fonction associée, , et , puisque alors , ?
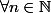
Est-ce qu'il est important d'utiliser le fait que Si alors , la première bissectrice ?

[deltab]

Après avoir étudié la fonction associée, , et , puisque alors , ?
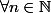
Est-ce qu'il est important d'utiliser le fait que Si alors , la première bissectrice ?

On a , il est superflu d'écrire l'exposant. Moi-même j'ai repris l'écriture (par fainéantise?) en faisant du copier-coller.
Recalcules f(e-1) (f(e-1)=0 ne te semple-il pas bizarre?)
As-tu montrer qu'effectivement on a: .
Le fait que cette implication soit importante ou pas dépend des questions posées, questions que je ne connais pas encore.

[lopilu]

Je met l'exposant car ma professeur est assez pointilleuse sur ces petits détails en fait...
Oups non pardon je m'étais trompé, f(e-1)=e-1, ça me semblais bizarre effectivement. J'ai confondu avec lorsque x=e-1, alors f(x)=x.
Oui dans la Partie I de l'exercice, il était demandé de faire une étude complète de la fonction associée à et notamment d'étudier la position relative de par rapport à la première bissectrice y=x.

[deltab]

Je met l'exposant car ma professeur est assez pointilleuse sur ces petits détails en fait...
Oups non pardon je m'étais trompé, f(e-1)=e-1, ça me semblais bizarre effectivement. J'ai confondu avec lorsque x=e-1, alors f(x)=x.
Oui dans la Partie I de l'exercice, il était demandé de faire une étude complète de la fonction associée à et notamment d'étudier la position relative de par rapport à la première bissectrice y=x.

Si c'est le cas , quelle propriété peut-on déduire pour la suite

PS: je vais m'absenter pour un bon moment, désolé

[lopilu]

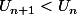
Si , donc donc , donc la suite est décroissante et par conséquent car
Super j'ai compris, merci infiniment de ton aide ! :we:

[deltab]

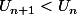
Si , donc donc , donc la suite est décroissante et par conséquent car
Super j'ai compris, merci infiniment de ton aide ! :we:

J'espère que tu as pu terminer l'exercice.
L'étude de la fonction permettait de conclure que si alors pour tout ,
L'étude du signe de donnait la décroissance de
Qu'as tu trouvé pour

[lopilu]

Oui c'est exactement ce que j'ai fais et j'ai pu terminer l'exercice !
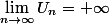
, donc si alors la suite est croissante.
En tout cas merci beaucoup pour ton aide !

[deltab]

Salut

Oui c'est exactement ce que j'ai fais et j'ai pu terminer l'exercice !
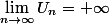
, donc si alors la suite est croissante.
En tout cas merci beaucoup pour ton aide !

Malheureusement c'est tout faux.
Tu avais trouvé que était décroissante et c'était juste, tu me dis maintenant qu'elle croissante.
De plus tu a montré (? je n'ai pas tout relu) que la fonction vérifiait et donc si est dans I alors reste dans I. Comment se fait-il que ?.
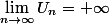
Je te laisse te corriger.

[lopilu]

Non pardon j'ai confondu. Car dans la suite de mon exercice on me demande lorsque , dans ce cas est croissante. Mais concernant l'intervalle j'ai réussi à correctement conclure.
Décidément, ça ne m'arrange pas d'écrire des maths sur ordinateur...