Intégrale et équation fonctionnelle
Olympiades mathématiques, énigmes et défis
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 31 Aoû 2006, 23:18
par nekros » 31 Aoû 2006, 23:18
Salut :happy3:
Soit
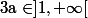
.
Trouver toutes les applications

de
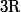
dans
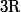
de classe
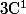
,
à valeurs positives (au sens large) telles que :
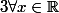
,
)^a= \int_0^x (f(t))^{a-1} dt)
A+
-
Bija
- Membre Naturel
- Messages: 12
- Enregistré le: 28 Aoû 2006, 19:22
-
 par Bija » 01 Sep 2006, 14:17
par Bija » 01 Sep 2006, 14:17
Si f(x) est différent de 0, en dérivant l'équation on obtient a*f'(x)=1.
On suppose f non nulle : f(x0) différent de 0. f est strictement positive au voisinage de x0, donc sur un intervalle du type [x0-c,x0+c[ et pour x dans cet intervalle, f(x)=(x-x0)/a+f(x0).
On en déduit que f est strictement positive sur un intervalle du type [y0,+inf[ avec f(x)=(x-y0)/a, pour x>y0.
f étant C1, f'(y0)=1/a et pour x au voisinage de y0, f(x) est équivalent à (x-y0)/a, donc f(x)<0 pour xcontradiction.
f=0 est la seule solution.
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 01 Sep 2006, 14:44
par nekros » 01 Sep 2006, 14:44
Salut,
f=0 est solution, mais ce n'est pas la seule.
Je pense que tu t'es trompé dans la dérivation.
A+
-
Bija
- Membre Naturel
- Messages: 12
- Enregistré le: 28 Aoû 2006, 19:22
-
 par Bija » 01 Sep 2006, 14:48
par Bija » 01 Sep 2006, 14:48
Une autre solution :
pour x<=0, l'intégrale du membre de droite est négative, donc f(x)=0 pour x<0.
Si f est non nulle soit x0 l'inf de {x/f(x)>0}. f est nulle sur [0,x0] et f'(x0)=0.
Soit n dans N*, il existe yn dans [x0,x0+1/n]/f(yn)>0, et donc f'(yn)=1/a.
Or yn tend vers x0 fonc f'(yn) tend vers f'(x0)=0 car f' est continue.
D'ou la contradiction.
EDIT : pour la dérivation j'obtiens a*f'(x)*f(x)^(a-1)=f(x)^(a-1).
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 01 Sep 2006, 14:58
par nekros » 01 Sep 2006, 14:58
J'espère que jme suis pas trompé en traitant l'exo :marteau:
Bon, pour la dérivée je suis d'accord.
Donc j'ai montré que f convient ssi f(0)=0 et f vérifie l'équation différentielle issue de la dérivation.
Puis on a
^' \ge 0)
donc f est croissante et on considère alors f^{-1}({0})
Je mets le raisnnement si tu veux.
A+
-
Bija
- Membre Naturel
- Messages: 12
- Enregistré le: 28 Aoû 2006, 19:22
-
 par Bija » 01 Sep 2006, 16:27
par Bija » 01 Sep 2006, 16:27
Oui poste ton raisonnement.
Et poste aussi le résultat final que tu obtiens, parce que je ne pense pas qu'il y ait d'autres solutions que la fonction nulle.
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 01 Sep 2006, 17:48
par nekros » 01 Sep 2006, 17:48
Ok,
Je crois que je me suis trompé, et que tu avais raison :marteau:

est solution équivaut à :
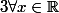
,
)^{a-1}f'(x)=(f(x))^{a-1})
et
=0)

est solution équivaut à :
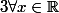
,
)^{a-1}(af'(x)-1)=0)
et
=0)
Or,
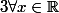
,
)^{a-1}(af'(x)-1)=0)
et
=0)
équivaut à
=0)
ou
=\frac{1}{a})
pour tout x
De là on en déduit que

est croissante.
Comme l'ensemble
)
( [ ] pour {}) est une partie fermée de

, puisque
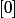
est un fermé de

et que f est continue, croissante alors c'est un intervalle de la forme ou
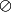
, ou
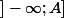
(A dans R) ou
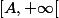
Pour le deuxième cas :
On a alors
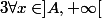
,
=\frac{1}{a})
donc
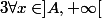
,
=\frac{x}{a}+b)
(b dans R)
Or,

est continue en
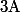
et
=0)
donc

(les autres cas sont plus simples)
Les solutions sont donc :
=\frac{x-A}{a})
si
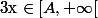
et
=0)
si
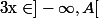
avec
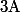
dans
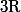
.
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 01 Sep 2006, 18:04
par nekros » 01 Sep 2006, 18:04
Ok
Je crois que je me suis trompé, et que tu avais raison :marteau:

est solution équivaut à :
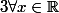
,
)^{a-1}f'(x)=(f(x))^{a-1})
et
=0)

est solution équivaut à :
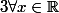
,
)^{a-1}(af'(x)-1)=0)
et
=0)
Or,
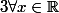
,
)^{a-1}(af'(x)-1)=0)
et
=0)
équivaut à
=0)
ou
=\frac{1}{a})
pour tout x
Je trouvais comme solution :
=\frac{x-A}{a})
si
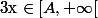
et
=0)
si
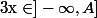
avec
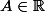
Mais cette solution ne fonctionne pas...
a+
-
Bija
- Membre Naturel
- Messages: 12
- Enregistré le: 28 Aoû 2006, 19:22
-
 par Bija » 01 Sep 2006, 18:55
par Bija » 01 Sep 2006, 18:55
Non parcequ'elle n'est pas C1.
Mais on peut restreindre les hypothéses et supposer f dérivable si tu veux.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 11 invités