Abérration
Olympiades mathématiques, énigmes et défis
-
upium666
- Membre Relatif
- Messages: 404
- Enregistré le: 14 Mai 2012, 21:44
-
par upium666 » 29 Aoû 2013, 07:57
Bonjour à tous et à toutes !
Voici le
lien du concours général de mathématiques - 2007
On considère l'Exercice 1
J'ai un petit hic concernant la compréhension de l'énoncé
Je résume le principe :
=T_0 \Leftrightarrow t:[-1;1] \rightarrow \mathbb{R})
)
où
 \in \mathbb{R}^3 : t(x)=ax^2+bx^2+c)
:
Soit
)
telle que
=f(x)+\lambda |g(x)|)
où
=Type(g)=T_{n-1})
Je n'ai pas eu de problème pour la première question, car j'ai établi que
=\frac{1}{2}x+\frac{1}{2}|x|)
Par contre, pour la deuxième question, voici mon problème :
On définit :
=0 \\ b(x)=0 \end{matrix}\right.)
=a'x^2+b'x^2+c')
et
=a''x^2+b''x^2+c'')
où
,(a'',b'',c'')) \in \{0\}^3 \times \{0\}^3)
, ce qui fait que
=Type(b)=T_0)
On définit maintenant :
=a(x)+1 \cdot |b(x)|)
alors
)
devrait être
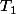
... or :
=0+1 \cdot |0|)
=0x^2+0x+0)
est de type
!
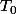
Cela m'empêche d'avancer dans mon raisonnement
Merci de m'éclaircir là-dessus !
-
Nuts13
- Messages: 2
- Enregistré le: 19 Sep 2013, 14:33
-
par Nuts13 » 19 Sep 2013, 14:38
Les fonctions f, g et S utilisées dans l'exemple sont exactement la même fonction.
Cette fonction fait partie de tous les Tn quel que soit n, ça ne lève pas forcément de contradiction et ne devrait pas gêner dans la résolution du problème.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
