Suite, raisonnement par récurrence

[butterfly22]

Bonjour, j'aurais besoin de votre aide pour un exercice sur le raisonnement par récurrence:

On considère la suite t(n) définie pour tout entier naturel n par t0=0et t(n+1)=t(n)+1/(n+1)(n+2)
Montrer que t(n)=n/(n+1)

Donc je fait un raisonnement par récurrence:

Nommons P(n) l'égalité "n/n+1)"

Initialisation
P(0)= 0/(0+1)=0/1 (je ne pense pas que ça soit ça mais je bloque dès l'initialisation)

Merci d'avance pour votre aide

[Sylviel]

Bonjour,

déjà il faudrait que P(n) soit une égalité, et non une fraction...

Ainsi P(0) doit être une égalité. Et tu dois initialiser en disant
tatata=tititi donc P(0) est vraie.

[butterfly22]

Donc ca donne:

Nommons P(n) l'égalité "t(n)=n/(n+1)"

Initialisation
t(0)=0 et t0=0/(0+1)=0
P(0) est vrai, P(n) est initialisé [C'est ca ?]

Hérédité
la je bloque complètement... :s

[Sylviel]

Tu veux montrer que, pour tout n, t(n)=n/(n+1). (c'est l'énoncé)
donc P(n) est l'égalité : " t(n)=n/(n+1)".

P(0) est donc l'égalité "t(0)=0/(0+1)"
or :
t(0)=0
0/(0+1)=0 donc t(0)=0/(0+1) donc P(0) est vraie.

(plus tard tu pourras écrire plus vite tout cela, mais là je t'expliques entièrement tout).

[butterfly22]

Je n'avais pas vu votre message avant d'avoir modifié le mien :s , pour l’initialisation je viens de comprendre par contre l'hérédité je bloque [ est ce qu'il faut remplacer tn par n/(n+1) dans l'expression de tn+1 ? mais pour quoi faire ? ]

[Sylviel]

C'est toujours la même chose pour la récurrence :

tu écris ce que tu as :

Supposons que P(n) soit vraie : t(n)=n/(n+1)

Puis ce que tu veux :

Montrons P(n+1) : t(n+1)=... / ...

(je te laisse compléter).

Et après tu réfléchis comment faire. A priori ici tu vas utiliser
t(n+1)=t(n)+1/(n+1)(n+2)
puis l'hypothèse de récurrence pour te débarasser de t(n).

[butterfly22]

Hérédité:
Supposons P(n) vrai a-t-on P(n)=n/(n+1)
Supposons P(n) vrai a-t-on P(n+1) vrai?
[je me mélange dans les supposons, est ce que c'est ça ?]

[Sylviel]

Oui tu te mélanges. Je t'ai donné tout le détail dans mon dernier message... Les deux phrases que j'ai mis en "quote" sont celles que tu dois écrire. La première chose que tu as à faire c'est d'expliciter P(n+1) c'est à dire de remplacer n par n+1 dans P(n).

[butterfly22]

Daccord
donc pour l'hérédité j'ai fait
tn+1=n/(n+1) + 1/(n+1)(n+2)
tn+1= n(n+2)/(n+1)(n+2) + 1/(n+1)n+2)
tn+1=(n²+2n+1)/(n²+3n+2)

Par contre pour simplifier je ne sais pas trop comment faire

[Sylviel]

Et bien si tu avais écris P(n+1) comme je te l'ai conseillé tu saurais ce que tu dois montrer. Pour simplifier il faut commencer par factoriser, et tu sais par quoi factoriser puisque tu connais les facteurs qui doivent rester (ce sont ceux de la fraction donnée par P(n+1)) :zen:

[butterfly22]

Pourquoi faut il factorisé ? moi j'aurais: éliminé les n² , enlever 2n au numérateur et dénominateur et enlever 1 au numérateur et dénominateur, il resterais donc n/(n+1)

[Sylviel]

J'ai très très peur quand je lis ce que tu écris.
J'ai l'impression que tu veux me simplifier a dans la fraction
, non ?

Ainsi d'après cette "règle" tu as
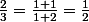:briques:

Donc pour rappel : on simplifie une fraction en enlevant un facteur commun. Si tu veux simplifier ta fraction tu dois donc factoriser pour avoir un truc de la forme
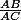d'où tu pourras simplifier le A.

[butterfly22]

DACCORD mais parcontre à partir d'où dois je factoriser, ca veux dire que ce que j'ai fait c'est tout faux ?

[Sylviel]

Je n'ai pas vérifié mais pour moi

tn+1=(n²+2n+1)/(n²+3n+2)

est juste.

Peux tu écrire P(n+1) (ce que tu veux montrer) s'il te plait ?
(Petite remarque : il faut commencer par écrire ce que tu veux montrer, pour avoir une idée d'où tu vas)

Ensuite tu essaie de factoriser le numérateur et le dénominateur pour voir un facteur commun (les deux autres étant donnés par ce que je t'ai demandé d'écrire) et simplifier par ce facteur commun.

[butterfly22]

Ce que je veux montrer:
P(n+1)=n/(n+1) + 1/(n+1)(n+2)

pour factoriser il faut calculer delta non ?

[Sylviel]

Non et non.

P(n) c'est une affirmation, une phrase, une assertion. Pas un nombre.

Si P(n) c'est : "t(n)=n/(n+1)"
alors
P(3) c'est "t(3)=3/(3+1)"
P(x) c'est "t(x)=x/(x+1)"
P(:doh: ) c'est "t(:doh: )=:doh: /(:doh: +1)"
donc
P(n+1) c'est B/C = ... / ...

Et pour factoriser je te l'ai dis plein de fois déjà :
une fois que tu auras écris P(n+1) tu auras la fraction B/C.
Pour le moment tu as la fraction AB/(AC). Donc une fois que tu auras écris P(n+1) tu pourras factoriser ton numérateur par B et ton dénominateur par C.

Tu peux aussi passer par le discriminant mais c'est vraiment shadok : pourquoi faire simple quand on peut faire compliqué...

[butterfly22]

Supposons P(k) vrai a t on P(k+1) vrai ?
Pk+1=(k+1)/(k+1+1) + 1/(k+1+1)(k+1+2)
Pk+1=(k+1)/(k+2) + 1/(k+2)(k+3)
Pk+1=((k+1)*(k+3)+1)/((k+2)(k+3))
Pk+1=(k²+4k+4)/(k²+6k+6)

c'est ca ? mais comment factoriser ?

[Sylviel]

Relis mon dernier message, mes derniers messages.

P(n) c'est une affirmation, une phrase, une assertion. Pas un nombre.

Tu ne m'as toujours pas écris ce qu'était P(n+1)... C'est la première chose à faire et que je te demander depuis le début.

[butterfly22]

bah comment fait on

[Sylviel]

Je me cite quelques message plus haut. Je ne sais pas quoi dire de plus :

P(n) c'est une affirmation, une phrase, une assertion. Pas un nombre.

Si P(n) c'est : "t(n)=n/(n+1)"

alors
P(3) c'est "t(3)=3/(3+1)"
P(x) c'est "t(x)=x/(x+1)"
P( :triste: ) c'est "t( :triste: )= :triste: /( :triste: +1)"
donc
P(n+1) c'est ... / ...