Trinôme du second degré
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Matheuseoupas
- Membre Naturel
- Messages: 81
- Enregistré le: 12 Déc 2012, 23:19
-
 par Matheuseoupas » 13 Sep 2013, 19:55
par Matheuseoupas » 13 Sep 2013, 19:55
Bonsoir les matheux !
J'ai un exercice sur les fonctions trinômes et voilà déjà plus d'une heure que je cherche..
Mais je n'avance pas ..
Merci d'avance pour votre aide :)
Ex: Déterminer une fonction trinôme du second degré tel que -2 et 3 sont les solutions de f(x)= 0
Voilà ! :D
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 13 Sep 2013, 19:57
par Sourire_banane » 13 Sep 2013, 19:57
Matheuseoupas a écrit:Bonsoir les matheux !
J'ai un exercice sur les fonctions trinômes et voilà déjà plus d'une heure que je cherche..
Mais je n'avance pas ..
Merci d'avance pour votre aide

Ex: Déterminer une fonction trinôme du second degré tel que -2 et 3 sont les solutions de f(x)= 0
Voilà !

Salut,
Tu sais qu'un trinôme du second degré est factorisable par ses racines réelles s'il en a.
-
Matheuseoupas
- Membre Naturel
- Messages: 81
- Enregistré le: 12 Déc 2012, 23:19
-
 par Matheuseoupas » 13 Sep 2013, 19:59
par Matheuseoupas » 13 Sep 2013, 19:59
Sourire_banane a écrit:Salut,
Tu sais qu'un trinôme du second degré est factorisable par ses racines réelles s'il en a.
Euh..?
Je ne comprends pas .. un exemple .?
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 13 Sep 2013, 20:00
par Sourire_banane » 13 Sep 2013, 20:00
Par exemple,
Peux-tu me dire en quels réels s'annule (2x-3)(8x+4) ?
-
Matheuseoupas
- Membre Naturel
- Messages: 81
- Enregistré le: 12 Déc 2012, 23:19
-
 par Matheuseoupas » 13 Sep 2013, 20:04
par Matheuseoupas » 13 Sep 2013, 20:04
Sourire_banane a écrit:Par exemple,
Peux-tu me dire en quels réels s'annule (2x-3)(8x+4) ?
Et bien je crois en 1,5 et -0,5 .?
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 13 Sep 2013, 20:05
par Sourire_banane » 13 Sep 2013, 20:05
Matheuseoupas a écrit:Et bien je crois en 1,5 et -0,5 .?
Bien.
Maintenant débrouille-toi pour construire un trinôme qui s'annule en x=a et en x=b.
-
Matheuseoupas
- Membre Naturel
- Messages: 81
- Enregistré le: 12 Déc 2012, 23:19
-
 par Matheuseoupas » 13 Sep 2013, 20:23
par Matheuseoupas » 13 Sep 2013, 20:23
Sourire_banane a écrit:Bien.
Maintenant débrouille-toi pour construire un trinôme qui s'annule en x=a et en x=b.
je cherche ..
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 13 Sep 2013, 20:36
par Sourire_banane » 13 Sep 2013, 20:36
Cherche, cherche.
C'est en se creusant la tête qu'on s'améliore.
-
Matheuseoupas
- Membre Naturel
- Messages: 81
- Enregistré le: 12 Déc 2012, 23:19
-
 par Matheuseoupas » 13 Sep 2013, 20:39
par Matheuseoupas » 13 Sep 2013, 20:39
bon je ne trouve vraiment pas .. y'a pas une façon "simple" et sur de réussir ce type d'exercice ?
-
Matheuseoupas
- Membre Naturel
- Messages: 81
- Enregistré le: 12 Déc 2012, 23:19
-
 par Matheuseoupas » 13 Sep 2013, 20:41
par Matheuseoupas » 13 Sep 2013, 20:41
Les trinômes du second degré ont plusieurs formes .. ici se serait du type (x+a)(x-b) ?
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 13 Sep 2013, 20:43
par Sourire_banane » 13 Sep 2013, 20:43
Matheuseoupas a écrit:Les trinômes du second degré ont plusieurs formes .. ici se serait du type (x+a)(x-b) ?
Presque, car dans ce cas t'aurais -a et b pour solutions de (x+a)(x-b)=0.
-
Matheuseoupas
- Membre Naturel
- Messages: 81
- Enregistré le: 12 Déc 2012, 23:19
-
 par Matheuseoupas » 13 Sep 2013, 20:46
par Matheuseoupas » 13 Sep 2013, 20:46
donc je peux dire que a = 2 et b = -3 ?
donc ma fonction est : (x+2)(x-3)=0
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 13 Sep 2013, 21:03
par Sourire_banane » 13 Sep 2013, 21:03
Matheuseoupas a écrit:donc je peux dire que a = 2 et b = -3 ?
donc ma fonction est : (x+2)(x-3)=0
Non, dommage. Essaie de résoudre ce truc que tu as écris pour x.
-
Matheuseoupas
- Membre Naturel
- Messages: 81
- Enregistré le: 12 Déc 2012, 23:19
-
 par Matheuseoupas » 13 Sep 2013, 21:10
par Matheuseoupas » 13 Sep 2013, 21:10
Sourire_banane a écrit:Non, dommage. Essaie de résoudre ce truc que tu as écris pour x.
J'ai pourtant essayer de faire en sorte que de trouver (x+a)=0 avec pour solution -2 .. donc -2+a =0
et a= 2 .?
Pareil pour 3 .. (x-b)=0 avec S :3 donc 3-b=0 .. -b=-3 donc 3=b
je ne comprends pas quelle est mon erreur ..
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 13 Sep 2013, 21:20
par Sourire_banane » 13 Sep 2013, 21:20
Euh oui désolé oups, l'expression est juste mais les valeurs de a et b ne le sont pas.
En effet on doit avoir (x-a)(x-b)=0 enfin bref.
-
Matheuseoupas
- Membre Naturel
- Messages: 81
- Enregistré le: 12 Déc 2012, 23:19
-
 par Matheuseoupas » 13 Sep 2013, 21:41
par Matheuseoupas » 13 Sep 2013, 21:41
Je ne comprends pas :/
A chaque fois que je repars de zéro je finis par retrouver les mêmes résultats ..
-
Archibald
- Membre Relatif
- Messages: 415
- Enregistré le: 05 Avr 2013, 17:06
-
 par Archibald » 13 Sep 2013, 21:41
par Archibald » 13 Sep 2013, 21:41
la forme factorisée d'un trinôme du second degré est plutôt
(x-x_2))
avec
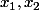
ses racines (ici
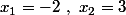
)
Mais bon, l'énoncé demande "
une fonction trinôme du second degré tel que -2 et 3 sont les solutions de f(x)= 0" donc on peut arbitrairement choisir n'importe quel

pourvu qu'il soit différent de zéro.
-
Matheuseoupas
- Membre Naturel
- Messages: 81
- Enregistré le: 12 Déc 2012, 23:19
-
 par Matheuseoupas » 13 Sep 2013, 22:00
par Matheuseoupas » 13 Sep 2013, 22:00
Je comprends encore moins ..
-
Matheuseoupas
- Membre Naturel
- Messages: 81
- Enregistré le: 12 Déc 2012, 23:19
-
 par Matheuseoupas » 13 Sep 2013, 22:02
par Matheuseoupas » 13 Sep 2013, 22:02
du coup mon trinôme c'est: a(x+2)(x-3)=0 .?
-
Archibald
- Membre Relatif
- Messages: 415
- Enregistré le: 05 Avr 2013, 17:06
-
 par Archibald » 13 Sep 2013, 22:25
par Archibald » 13 Sep 2013, 22:25
Oui ! (si tu m'enlèves ce "= 0" )
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités

