Bonsoir, j'ai un problème concernant un raisonnement par récurrence mais j'ai eu très peu de cours et d'exemples sur les récurrences.
Question :
Montrer par récurrence
Quelque soit n appartenant a N*
Somme de (n-1) a n de (K! . k) = (n+1)! - 1
Voilà ma récurrence je sais pas par quoi commencer l'initialisation ?
Merci a vous.
Montrer par récurrence
5 messages
- Page 1 sur 1
Bonjour.
Je suppose que tu as à démontrer que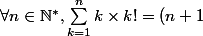!-1) et non
et non 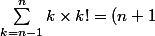!-1) (qui est d'ailleurs vérifiée pour n=1 et n=2 mais ne l'est plus à partir de n=3, le 1er membre est un nombre pair et le second est impair).
(qui est d'ailleurs vérifiée pour n=1 et n=2 mais ne l'est plus à partir de n=3, le 1er membre est un nombre pair et le second est impair).
Avec ces nouvelles données,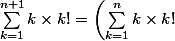+(n+1)(n+1)!) .
.
Continues!
roro60 a écrit:J'ai fais l'initialisation mon problème vient surtout de l'hérédité, je sais pas quand il faut utiliser l'hypothèse de récurrence.
Merci
Je suppose que tu as à démontrer que
Avec ces nouvelles données,
Continues!
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
