Petit exo sur la commutativité d'un groupe

[kingsize]

Bonjour,

Voici un exo sur les groupes sur lequel je sèche :

Soit G un groupe de loi notée multiplicativement. On suppose que l'application x -> x^3 est un endomorphisme surjectif de G. Montrer que G est commutatif.

Voici ce que j'ai fait :
Puisque x -> x^3 est surjectif, il suffit de montrer que x^3 et y^3 commutent pour tout x, y dans G.
J'ai alors écrit x^3 . y^3 = (xy)^3 car x -> x^3 est un morphisme de G
= (xy)². xy
=y².x².xy car (xy)² = y².x² (démonstration triviale)

Il suffit alors de montrer que x^3 .y = y. x^3 mais cela revient à résoudre l'exo puisque x -> x^3 est surjective !
Si quelqu'un a une piste, je suis preneur.
Merci. :happy2:

[kingsize]

comme je l'ai dit, on obtient facilement (xy)² = y².x²
Je pense que ça doit bien servir quelque part...

[jlb]

comme je l'ai dit, on obtient facilement (xy)² = y².x²
Je pense que ça doit bien servir quelque part...

Bonsoir, je remonte l'exo si une bonne âme a une piste, j'ai bien cherché mais je ne trouve pas la direction!! Merci.

[arnaud32]

un element de reponse:

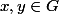
Soient quelconques.
De, on déduit puis et donc
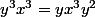
, ce qui donne .

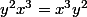
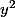
Ainsi, pour tout y dans G commute à tous les éléments de la
forme avec x dans G.
d'ou avec la 'propriete de surjectivite du cube' :
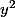
pour tout y dans G commute à tous les éléments de G

[Doraki]

Soit a et b quelconques dans G et soit c l'inverse de b.

Alors :
baaa(baaa)baaa
= bbbaaaaaaaaa
= bbbaaaaaabcaaa
= baabaabaabcaaa
= baaaaaabbbcaaa
= baaa(aaab)baaa

Et donc baaa = aaab.
La surjectivité de a -> a^3 conclut.

[jlb]

merci beaucoup!! c'est clair maintenant pour moi. je n'étais par contre pas près de trouver!!! par curiosité, c'est un truc classique ou vous avez cherché un peu? merci encore, à bientôt!!