Exo Suites TS
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
BouleDeFeu
- Messages: 4
- Enregistré le: 04 Sep 2013, 15:45
-
 par BouleDeFeu » 04 Sep 2013, 15:52
par BouleDeFeu » 04 Sep 2013, 15:52
Bonjour, j'ai un exo sur les suites et depuis maintenant une heure je tourne en rond ! Donc je vous explique la situation : On pose U0=1. Pour tout n appartenant a N , on a Un+1=3Un-6 et Vn=Un-3.
J'ai donc calculé les 20 premiers termes des deux suites, jusque la tout va bien.
U0=1
U1=-3
U2=-15
U3=-51
U4=-159 etc ...
V0=-2
V1=-6
V2=-18
V3=-54
V4=-162 etc ...
Et je dois donc conjecturer Un et Vn en fonction de n mais je n'y arrive pas.
Comment faire ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 04 Sep 2013, 16:14
par chan79 » 04 Sep 2013, 16:14
Bonjour
Tu devrais calculer

-
BouleDeFeu
- Messages: 4
- Enregistré le: 04 Sep 2013, 15:45
-
 par BouleDeFeu » 04 Sep 2013, 16:23
par BouleDeFeu » 04 Sep 2013, 16:23
Oui mais cela me permet de calculer la raison (q) qui est 3. ( je suis vraiment pas doué pour les suites j'ai rater presque tout le chapitre a cause de pb médicaux) la raison peut-elle m'aider a conjecturer Vn et Un en fonction de n )
-
Titahn
- Membre Relatif
- Messages: 282
- Enregistré le: 06 Mar 2013, 15:51
-
 par Titahn » 04 Sep 2013, 16:38
par Titahn » 04 Sep 2013, 16:38
BouleDeFeu a écrit:Oui mais cela me permet de calculer la raison (q) qui est 3. ( je suis vraiment pas doué pour les suites j'ai rater presque tout le chapitre a cause de pb médicaux) la raison peut-elle m'aider a conjecturer Vn et Un en fonction de n )
Brièvement parce que j'suis à la bourre :
En effet la raison est 3. Et une suite géométrique de raison q est définie comme Vn+1 = q*Vn
Et par extension Vn=(q^n)*V0
Ici, faut que tu trouves toi même la forme de Un, mais elle n'est pas très compliquée, quelques tatonnages et ça devrait passer. En indice, sa forme est Un+1=a * Un + b
À toi de trouver a et b !

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 04 Sep 2013, 16:57
par chan79 » 04 Sep 2013, 16:57
on sait que
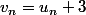
donc, connaissant

, on obtient

-
BouleDeFeu
- Messages: 4
- Enregistré le: 04 Sep 2013, 15:45
-
 par BouleDeFeu » 04 Sep 2013, 17:06
par BouleDeFeu » 04 Sep 2013, 17:06
Donc si j'ai bien compris, sachant que Vn=(q^n)*V0 et que Vn = Un-3, (q^n)*V0=Un-3 puis en faisant du 'passe-passe' on obtient : Un=(q^n)*V0+3 ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 04 Sep 2013, 17:20
par chan79 » 04 Sep 2013, 17:20
BouleDeFeu a écrit:Donc si j'ai bien compris, sachant que Vn=(q^n)*V0 et que Vn = Un-3, (q^n)*V0=Un-3 puis en faisant du 'passe-passe' on obtient : Un=(q^n)*V0+3 ?
oui, sachant qu'il faut remplacer q et

par leurs valeurs
-
BouleDeFeu
- Messages: 4
- Enregistré le: 04 Sep 2013, 15:45
-
 par BouleDeFeu » 04 Sep 2013, 17:29
par BouleDeFeu » 04 Sep 2013, 17:29
chan79 a écrit:oui, sachant qu'il faut remplacer q et

par leurs valeurs
Donc Un=3^n*(-2)+3 Merci beaucouuuup !!!

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 04 Sep 2013, 17:35
par chan79 » 04 Sep 2013, 17:35
BouleDeFeu a écrit:Donc Un=3^n*(-2)+3 Merci beaucouuuup !!!
c'est bien ça
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
