[TEX]F\subset(F^\perp)^\perp[/TEX] ?
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
AshEnVaLe
- Messages: 4
- Enregistré le: 29 Aoû 2006, 09:56
-
 par AshEnVaLe » 29 Aoû 2006, 10:11
par AshEnVaLe » 29 Aoû 2006, 10:11
Bonjour,
J'avais une quesiton quant aux espaces vectoriels muni d'un produit scalaire de dimension infinie. Est ce que la propriété
^\perp)
est vrai dans un espace non euclidien comme défini ci-dessus ?
Je pensais que oui, mais un exemple simple la contredit (à moins que ça soit cette preuve qui soit erronée !) :
Plaçons nous dans K[X] muni du produit scalaire
\mapsto(P|Q)=(\sum_ia_iX^i|\sum_ib_iX^i)=a_0b_0)
Cette application est bien bilinéaire symétrique (de par la commutativité de la loi x dans K[X]), et positive :
\geq0)
.
Cependant, prenons X, ce vecteur est orthogonal à n'importe quel vecteur de K[X]. donc

d'où
^\perp={0})
Or

!!
So ? Ou est le probleme ?
Merci d'avance
AshEnVaLe
-
AshEnVaLe
- Messages: 4
- Enregistré le: 29 Aoû 2006, 09:56
-
 par AshEnVaLe » 29 Aoû 2006, 10:18
par AshEnVaLe » 29 Aoû 2006, 10:18
Je crois avoir trouvé le problème de la preuve :
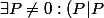=0)
Mais je ne comprends toujours pas la raison de
^\perp)
-
El_Gato
- Membre Relatif
- Messages: 313
- Enregistré le: 09 Fév 2006, 17:07
-
 par El_Gato » 29 Aoû 2006, 10:20
par El_Gato » 29 Aoû 2006, 10:20
Ta forme est bien positive, mais elle ne l'est pas strictement. Donc il y a des vecteurs isotropes (typiquement les polynomes de degré >= 1) et l'orthogonal de K[X] n'est pas {0}.
-
Yipee
- Membre Relatif
- Messages: 256
- Enregistré le: 15 Déc 2005, 07:34
-
 par Yipee » 29 Aoû 2006, 10:22
par Yipee » 29 Aoû 2006, 10:22
Ta forme bilinéaire n'est pas un produit scalaire car elle n'est pas définie. De ce fait l'orthogonal de
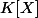
n'est pas 0. Il y a par exemple

dedans...
-
El_Gato
- Membre Relatif
- Messages: 313
- Enregistré le: 09 Fév 2006, 17:07
-
 par El_Gato » 29 Aoû 2006, 10:24
par El_Gato » 29 Aoû 2006, 10:24
AshEnVaLe a écrit:Mais je ne comprends toujours pas la raison de
^\perp)
Cette relation est vraie dans tout espace préhilbertien: si

alors pour tout

=0. D'où le résultat.
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 29 Aoû 2006, 11:53
par nekros » 29 Aoû 2006, 11:53
Tu peux le montrer de cette manière :
Soit

dans

, soit
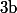
dans

. On a donc
=0)
.
Donc

,
=0)
et donc
^\perp)
Sauf erreurs.
A+
-
AshEnVaLe
- Messages: 4
- Enregistré le: 29 Aoû 2006, 09:56
-
 par AshEnVaLe » 30 Aoû 2006, 15:02
par AshEnVaLe » 30 Aoû 2006, 15:02
El_Gato a écrit:Cette relation est vraie dans tout espace préhilbertien: si

alors pour tout

=0. D'où le résultat.
Je suis peut être stupide, ou il y a un déclic :id: qui ne s'est pas fait dans ma tête, mais je ne comprends pas en quoi ce qui est cité explique
^\perp)
.
Merci d'expliciter :hein:
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 30 Aoû 2006, 15:14
par nekros » 30 Aoû 2006, 15:14
Salut,
Soit

dans

, soit

dans

, on a
=0)
. On en déduit que

,
=0)
, c'est-à-dire
^\perp)
A+
-
xon
- Membre Relatif
- Messages: 100
- Enregistré le: 24 Aoû 2006, 14:57
-
 par xon » 30 Aoû 2006, 15:19
par xon » 30 Aoû 2006, 15:19
En fait cela veut dire que tout vecteur

est orthogonal à tout

, donc F tout entier est orthogonal à
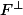
et donc
^\perp)
.
Je suis pas sur d'avoir été plus clair...
-
El_Gato
- Membre Relatif
- Messages: 313
- Enregistré le: 09 Fév 2006, 17:07
-
 par El_Gato » 30 Aoû 2006, 15:24
par El_Gato » 30 Aoû 2006, 15:24
En dimension finie, tu as toujours
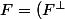^{\perp})
.
C'est en dimension non-finie que l'inclusion peut être stricte: elle traduit alors des conditions de nature topologique.
Par exemple dans un Hilbert, de dimension non-finie, l'égalité a bien lieu, et elle est équivalente à la caractérisation des formes linéaires continues qui sont toujours "réalisées" par un produit scalaire avec un certain vecteur. C'est cette petite subtilité qui fonde l'utilité des Hilbert en analyse.
Mais dans les espaces préhilbertiens généraux (non complets), l'inclusion peut être stricte.
-
AshEnVaLe
- Messages: 4
- Enregistré le: 29 Aoû 2006, 09:56
-
 par AshEnVaLe » 30 Aoû 2006, 16:16
par AshEnVaLe » 30 Aoû 2006, 16:16
J'ai très bien compris à présent. Merci à vous tous pour vos réponses.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
