Bonjour, et bonne rentrée.
Je suis tombé sur cette formule (dite formule de Rodriguès) que j'essaye de démontrer
^n=\frac1{2\pi}\int_{-\pi}^{\pi}(x+i\sqrt{1-x^2}\sin\theta)^nd\theta)
Voici où j'en suis dans la démo :
- Les puissances impaires de

dans le développement de droite correspondent à des puissances impaires de
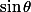
qui, intégrées entre
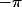
et

donnent un résultat nul, éliminant du même coup les radicaux. Le membre de droite est bien un polynome réel de degré

.\\
- Pour
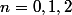
on obtient respectivement

,

et

dans les 2 membres, ce qui initialise la récurrence.\\
- J'ai écrit que
^{n+1}=\frac{d^n}{dx^n}\frac d{dx}(x^2-1)^{n+1}=2(n+1)\frac{d^n}{dx^n}x(x^2-1)^n)
ce qui donne par Leibniz
(x\frac{d^n}{dx^n}(x^2-1)^n+n\frac{d^{n-1}}{dx^{n-1}}(x^2-1)^n))
\\
et c'est ce dernier terme qui pose problème.
Peut être la récurrence n'est-elle pas la solution ...
Merci de vos avis
