Nombres complex

[activee]

Quelqu'un peut il m'aider pour resoudre ceci : (a+bi)² > 6. Donnez toutes les valeurs de a et b pour que ceci soit vrai.

J'ai réaliser une ébauche pour répondre a cet exercice, mais ça n"a ni queu ni tête.

Mon ebauche :

bi = u | u € R =>

b = k i^x | k € R , x est impaire (je sais pas comment on écrit cela en language math. Si x est impaire alors u € R.

Le probleme c'est que si x = {1,5,9,13,...}, alors u sera negatif si k > 0, positif si k< 0 et 0 si k = 0; (de nouveau je ne sais pas comment écrire cela en language math). Etc. Donc voila je suis un peut perdu merci de l'aide

[jlb]

bonjour, a et b sont dans quel domaine? réels, complexes? si réels, développe et regarde les conditions à avoir pour que cela ait du sens. si complexes, pose a=x_a+iy_a et b=x_b+iy_b avec x_a,y_a,x_b,y_b réels, et retrouve la méthode précédente .

[activee]

bonjour, a et b sont dans quel domaine? réels, complexes? si réels, développe et regarde les conditions à avoir pour que cela ait du sens. si complexes.

Dans le domaine réel. J'avais même pas vu.


La réponse est donc impossible ?

[jlb]

Dans le domaine réel. J'avais même pas vu.


La réponse est donc impossible ?

dans ce cas (a+ib)²=a²+2iab+(bi)²=a²-b²+2iab et donc pour que l'exo ait du sens ( il n'y a pas d'ordre dans C): 2ab=0 soit a=0 ou b=0 et l'exo devient facile: 1er cas a=0: -b²>6 pas de solution 2eme cas b=0 donc a²>6 soit a>racinecarrée(6) ou a<-racinecarrée(6).

[activee]

dans ce cas (a+ib)²=a²+2iab+(bi)²=a²-b²+2iab et donc pour que l'exo ait du sens ( il n'y a pas d'ordre dans C): 2ab=0 soit a=0 ou b=0 et l'exo devient facile: 1er cas a=0: -b²>6 pas de solution 2eme cas b=0 donc a²>6 soit a>racinecarrée(6) ou a<-racinecarrée(6).

MERCI 1000 fois

[deltab]

Bonjour.

[quote="jlb"]dans ce cas (a+ib)²=a²+2iab+(bi)²=a²-b²+2iab et donc pour que l'exo ait du sens ( il n'y a pas d'ordre dans C): 2ab=0 soit a=0 ou b=0 et l'exo devient facile: 1er cas a=0: -b²>6 pas de solution 2eme cas b=0 donc a²>6 soit a>racinecarrée(6) ou a0[/TEX], en multipliant les 2 membres de l'inégalité par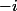, elle ne vas changer de sens d'où , 1 serait négatif

Quand on compare

[deltab]

Bonjour.

[quote="jlb"]dans ce cas (a+ib)²=a²+2iab+(bi)²=a²-b²+2iab et donc pour que l'exo ait du sens ( il n'y a pas d'ordre dans C): 2ab=0 soit a=0 ou b=0 et l'exo devient facile: 1er cas a=0: -b²>6 pas de solution 2eme cas b=0 donc a²>6 soit a>racinecarrée(6) ou a 0[/TEX], en multipliant les 2 membres de l'inégalité par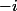, elle ne vas changer de sens d'où _ 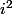[TEX] 6 et cette équation a un sens, on compare 2 nombres réels.

[jlb]

Bonsoir, ce que tu as écris m'intéresse au plus au point, je ne suis pas expert et j'aime comprendre. Ainsi, si j'ai tout compris, je peux écrire 5<6 ( en considérant 5 et 6 comme réels) mais c'est une faute d'écrire d'écrire 5+0i <6 +0i ( en considérant 5 et 6 comme complexes).

Ce qui m'ennuie, c'est que (3+0i)²=9>6, j'ai donc trouvé un couple (a,b) pour lequel l'inéquation est vérifiée et a du sens, je compare bien deux réels, non?. Mais la réponses est " l'inéquation n'a pas de sens, il n'y a pas de solution".
Je pensais qu'il était licite de définir "le domaine de définition" de l'inéquation: (a+ib)² est réel et sous cette condition, rechercher des solutions. [En gros, la relation d'ordre sur C sous entendue serait: z

[deltab]

[quote="jlb"]Bonsoir, ce que tu as écris m'intéresse au plus au point, je ne suis pas expert et j'aime comprendre. Ainsi, si j'ai tout compris, je peux écrire 5 0 alors ac 0 alors ac > bc

Voir les exemples donnés plus haut qui conduisent à des contradictions.

C'est pour ça qu'il n'a pas été défini de relation d'ordre sur C. il n'y a donc pas lieu de résoudre des "inégalités" dans C.

L'énoncé conforme à ce tu ou vous avez fait serait: Déterminer les nombres complexes a+bi tels que (a+bi)^2 soit réel puis parmi eux ceux vérifiant (a+bi)^2>6, l'écriture (a+bi)^2>6 est licite puisqu'on suppose que (a+bi)^2 est réel et on compare donc 2 réels.

[jlb]

en considérant la relation d'ordre partiel sur C "zRy si z et y sont réels avec zA priori, je pensais que, pour ce type de problème, cela était sous-entendu pour avoir du sens mais apparemment ce n'est pas le cas!!! Merci.

[activee]

Bonjour.


On avait peut-être |(a+bi)^2|>6 et cette équation a un sens, on compare 2 nombres réels.

l'equation était : Déteterminer toutes les valeurs réelles de a et b pour que (a+bi)² soit un réel strictement supérieur a 6. C'est moi qui l'ait retranscripte sous forme mathématique. La facon dont je l'avait écrite était-elle fausse ?


L'exercice réel était avec (a + bi)³ je viens de voir.

Puis-je écrire ceci comme cela ? :
(a + bi)³ > 6 .

donc : a³+3a²bi-3ab²+b³i³ > 6. Donc a ³ > 6. Donc b = 0 et a € R excepté dans l'interval compris entre - racine cubique de 6 et + racine cubique de 6.

[jlb]

.

Puis-je écrire ceci comme cela ? :
(a + bi)³ > 6 .

NON plutôt Re[(a + bi)³]>6 et Im[(a + bi)³] =0

donc : Re(a³+3a²bi-3ab²+b³i³) > 6. Donc a ³ -3ab²> 6 et 3a²b-b³=0 soit b(3a²-b²)=0 et a ³ -3ab²> 6

1er cas b=0 et donc a³>6 donc ...
2eme cas 3a²=b² et -8a³>6 donc....

( et je te conseille de représenter la fonction cube pour résoudre ces inéquations)
[je corrige, là, c'est un oubli, merci Deltab]

[deltab]

Bonjour

.

Puis-je écrire ceci comme cela ? :
(a + bi)³ > 6 .

NON plutôt Re[(a + bi)³]>6

donc : Re(a³+3a²bi-3ab²+b³i³) > 6. Donc a ³ -3ab²> 6 et 3a²b-b³=0 soit b(3a²-b²)=0 et a ³ -3ab²> 6

1er cas b=0 et donc a³>6 donc ...
2eme cas 3a²=b² et -8a³>6 donc....

( et je te conseille de représenter la fonction cube pour résoudre ces inéquations)

C'est encore NON pour plutôt Re[(a + bi)³]>6
Il manque la condition (a + bi)³ est réel condition équivalente à Im(a + bi)³=0

Résoudre seulement l'équation Re[(a + bi)³]>6 revient à trouver les nombres complexes a+bi dont la partie réelle de leur cube est >6 et un nombre complexe de partie réelle >6 n'implique pas que lui-même est réel, exemple 7+2i, autre exemple pour ,on a , on a mais 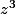lui n'est pas réel.

[alejandra]

Salut tout le monde bon je ne suis pas sur d'être au bon endroit, mais je suis nouvelle je suis désespérée depuis cette aprem j'éssais de réfléchir mais comme je déteste les maths et que la physique c'est un peu des maths et bien j'ai bo essayer de réfléchir je n'arrive pas meme quand on m'explique c'est un désastre ...Bon c'est un exercice normal selon la prof,mais c'est une térrible torture pour moi vu que je suis nul quelqu'un pourrais m'aider svp
voila
Le tableau ci-dessous présente les rayons R des orbites supposées circulaires de quelques planètes et leur temps de révolution T autour du Soleil.


Nom de la planéte : Mercure
Rayon de l'orbite(km) : 5,8 * 107
Temps de révolution (jours): 88

Nom de la planéte : Mars
Rayon de l'orbite(km) : 2,3 * 108
Temps de révolution (jours): 687

Nom de la planéte : Uranus
Rayon de l'orbite(km) : 2,9 * 109
Temps de révolution (jours): 30 700

1) Calculez, en km, la circonférence des orbites de chacune de ces planètes.
2) Calculez, en km/s, la vitesse de déplacement de chaque planète autour du Soleil.
3) Comment varient ces vitesses de déplacement autour du Soleil selon que les planètes en sont plus ou moins éloignées?

[Kiocle]

Bonjour, on pourrait noter l'ensemble des solutions comme :


L'écriture est acceptable car

l'ensemble des complexes qui sont réel une fois élevé au cube est :



ensuite il faut voir les conditions sur r et k pour que ce réel soit supérieur à 6.
deja si k est impair, si k est paire,
ensuite il faut que
Puis tu peux repasser sous forme a+ib

[deltab]

Bonjour, on pourrait noter l'ensemble des solutions comme :


L'écriture est acceptable car

l'ensemble des complexes qui sont réel une fois élevé au cube est :



ensuite il faut voir les conditions sur r et k pour que ce réel soit supérieur à 6.
deja si k est impair, si k est paire,
ensuite il faut que
Puis tu peux repasser sous forme a+ib

Pourquoi as-tu éliminé r=0? 0 est bien réel puisque Im(0)=0. 0 est éliminé ensuite par la condition Re(z^3)>6.

Remarque: Il n'y pas trop de difficulté à résoudre l'exercice sous forme algébrique c.à.d. à résoudre le système