Suites

[Sourire_banane]

Salut,
Si tu comptes bien, tu as n+1 termes.

Et attention, ce n'est pas une suite géométrique mais la somme partielle d'une suite géométrique.

[Kiocle]

Bonjour,

Et attention, ce n'est pas une suite géométrique mais la somme partielle d'une suite géométrique.

Il me semble aussi que c'est une suite géométrique de raison z^2

(z^2)^1 + (z^2)^2 + ... + (z^2)^n

[Sourire_banane]

Bonjour,


Il me semble aussi que c'est une suite géométrique de raison z^2

(z^2)^1 + (z^2)^2 + ... + (z^2)^n

C'est la somme partielle d'une suite donnée, très manifestement.

[Kiocle]

C'est la somme partielle d'une suite donnée, très manifestement.

Que veut tu dire par partielle?
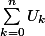
pour moi c'est avec :




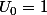
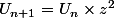
d'où

Ou est le problème dans cette somme et en quoi est elle partielle? cela m'intrique beaucoup.
La formule normale de la somme d'une suite géométrique me semble parfaitement convenir.

[Sourire_banane]

[url]http://fr.wikipedia.org/wiki/Série_(mathématiques)[/url]

La suite correspondante est (u_n)_N=(z^{2n})_N
La somme partielle d'ordre n correspondante est sum_{k<n+1} z^{2k}
La série associée est sum z^{2n}
La somme associée est sum_{n=0}^{infini} z^{2n}